gaussian-laplacian - 高斯模糊&拉普拉斯锐化

Posted on 2021-04-27 Edited on 2023-08-03 In cv , algo

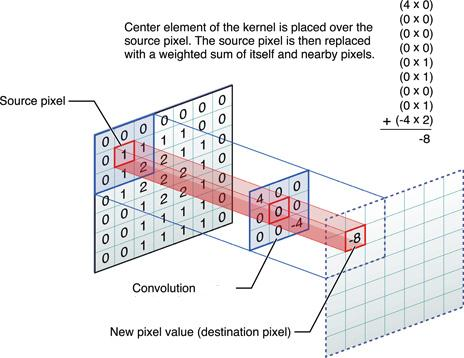
convolution operation on an image:

主要的卷积操作可以参考：
https://en.wikipedia.org/wiki/Kernel_(image_processing)
卷积的实际运算公式如下： $\displaystyle g(x,y)=\omega *f(x,y)=\sum _{dx=-a}^{a}{\sum _{dy=-b}^{b}{\omega (dx,dy)f(x+dx,y+dy)}}$

比较生动的图像如下：

高斯模糊

主要会生成一个高斯卷积核：with σ = 0.84089642, 一个7x7的kernel如下：
$$
\begin{matrix}
0.00000067 & 0.00002292 & \bold0.00019117 & 0.00038771 & \bold0.00019117 & 0.00002292 & 0.00000067 \
0.00002292 & 0.00078633 & 0.00655965 & 0.01330373 & 0.00655965 & 0.00078633 & 0.00002292 \
\bold0.00019117 & 0.00655965 & 0.05472157 & 0.11098164 & 0.05472157 & 0.00655965 & \bold0.00019117 \
0.00038771 & 0.01330373 & 0.11098164 & \bold0.22508352 & 0.11098164 & 0.01330373 & 0.00038771 \
\bold0.00019117 & 0.00655965 & 0.05472157 & 0.11098164 & 0.05472157 & 0.00655965 & \bold0.00019117 \
0.00002292 & 0.00078633 & 0.00655965 & 0.01330373 & 0.00655965 & 0.00078633 & 0.00002292 \
0.00000067 & 0.00002292 & \bold0.00019117 & 0.00038771 & \bold0.00019117 & 0.00002292 & 0.00000067
\end{matrix}
$$

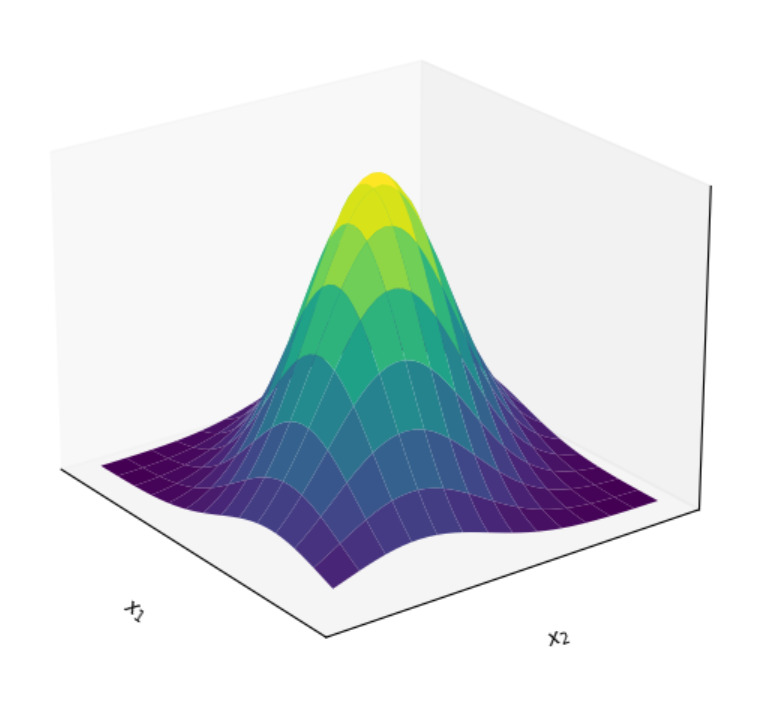
1个2d 正太分布的概率图：

高斯模糊的原理的理解：
对图像中的每一个像素做卷积(先乘后和)后，可以起到模糊的作用，主要原因是，高斯核中间位置的权重高（这也就是正太分布的性质），然后边缘的权重低，所以做完卷积获得的每一个新的像素都是其原来对应位置的像素和其周边的像素的加权和，能产生模糊感来自于周围像素的权重，能保证图像还有原来的样子是因为中间权重最大。如上的高斯核，可以清楚的看到高斯核最中心的概率是最大的。

lap锐化：

首先看一个图：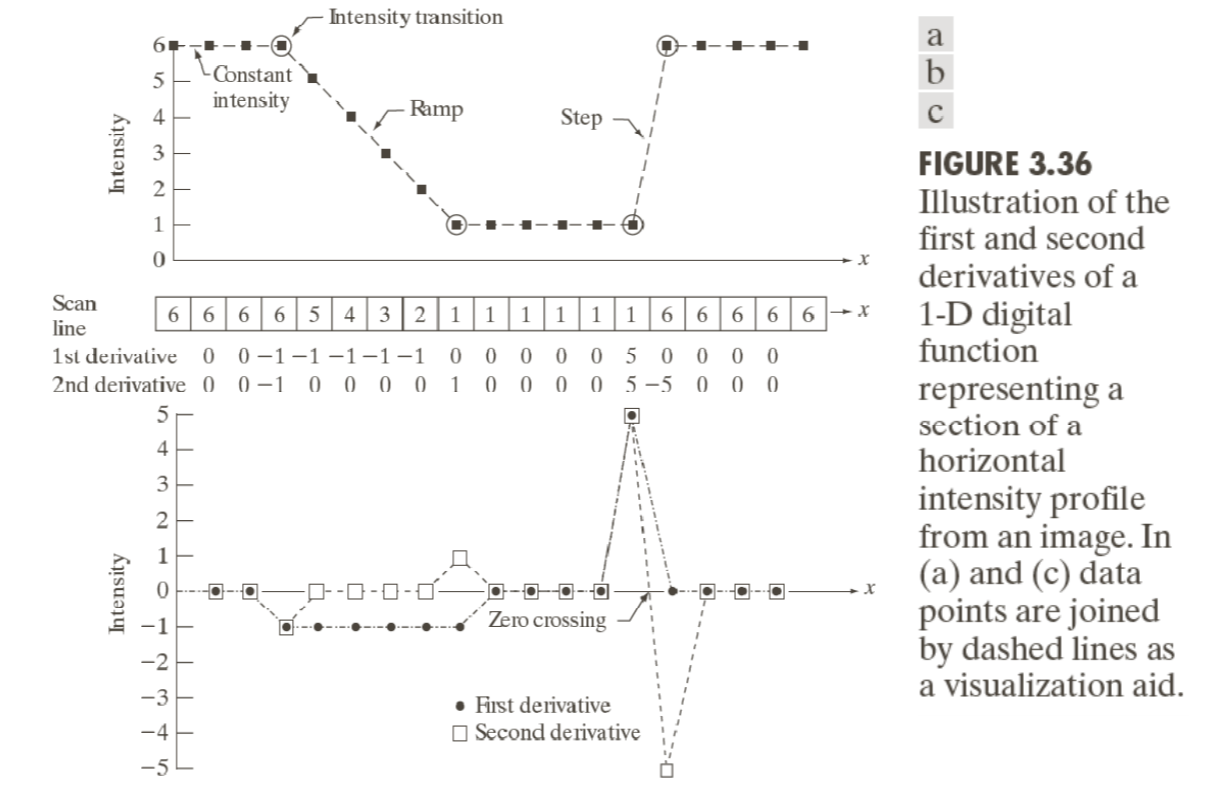

我们主要看下面的部分，first derivative和second derivative的折线对比，可以看到：
在ramp过程中，我们可以理解为朝着x方向，某种颜色从高过度到低，然后一阶导的反应就是这个过度的过程中的值都是一样的，所以这不利于探测出这样颜色持续变化的边界，于是使用2阶导，我们利用1阶导和2阶导的对比来验证这一点，可以得出之前一阶导2阶导对比里面1阶导用的核为：
$$
{\frac {\partial f}{\partial x}} = f(x+1) - f(x)

\Longrightarrow

\left {
\begin{matrix}
0 & 0 & 0 \
0 & 2 & -1 \
0 & -1 & 0
\end{matrix}
\right }
$$
下图中，左侧为2阶，右侧为1阶，可以看出2阶能够更好反应边界;

2阶导求解过程: (实际也就是分别对x,y做2阶偏导求和)， $\nabla f={\frac {\partial ^{2}f}{\partial x^{2}}}+{\frac {\partial ^{2}f}{\partial y^{2}}}$ ，对于离散的图片，其离散的二阶导应该为对x，和y分别求2阶导然后求和:
$$

\left {
\begin{aligned}
{\frac{\partial ^{2}f}{\partial ^{2}x}} = f(x+1, y) + f(x-1, y) - 2f(x,y) \
{\frac{\partial ^{2}f}{\partial ^{2}y}} = f(x, y+1) + f(x, y-1) - 2f(x,y)
\end{aligned}
\right.

\Longrightarrow

\nabla f={\frac {\partial ^{2}f}{\partial x^{2}}}+{\frac {\partial ^{2}f}{\partial y^{2}}} = f(x+1, y) + f(x-1, y) + f(x, y+1) + f(x, y-1) - 4f(x,y)
$$

于是可以得到，上述2阶导对应核为：
$$
\begin{matrix}
0 & -1 & 0 \
-1 & 4 & -1 \
0 & -1 & 0 \
\end{matrix}
$$

总的对比图：

这里贴上代码：

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
img = cv.imread('F:/myFiles/blogs/source/_posts/imageFiltering/index3.png')

# averaging blur
avKer = np.ones((5,5), np.float32) / 25
blur = cv.filter2D(img, -1, avKer)

# gaussian blur
# do the convolution manually
gKernel = cv.getGaussianKernel(3, 2)
print(gKernel[0:2])
blur2 = cv.filter2D(img, -1, gKernel)
# blur2 = cv.GaussianBlur(img, (5,5), 0)

# sharpenning
sharpKer = np.zeros((3,3), np.float32)
sharpKer[0] = [0, -1, 0]
sharpKer[1] = [-1, 5, -1]
sharpKer[2] = [0, -1, 0]
print(sharpKer)
sharp1 = cv.filter2D(img, -1, sharpKer)

# only using 1 derivative to get the edge:
oneDKer = np.zeros((3,3), np.float32)
oneDKer[0] = [0, 0, 0]
oneDKer[1] = [0, -2, 1]
oneDKer[2] = [0, 1, 0]
sharp2 = cv.filter2D(img, -1, oneDKer)

# laplacian
lap1 = cv.Laplacian(img, -1, None, 5)

# sobel
sob1 = cv.Sobel(img, -1, 1, 0, None, 5)
sob2 = cv.Sobel(img, -1, 0, 1, None, 5)

plt.subplot(331),plt.imshow(img),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(332),plt.imshow(blur),plt.title('Blurred - averaging')
plt.xticks([]), plt.yticks([])
plt.subplot(333),plt.imshow(blur2),plt.title('Blurred - gaussing')
plt.xticks([]), plt.yticks([])
plt.subplot(334),plt.imshow(sharp1),plt.title('sharp')
plt.xticks([]), plt.yticks([])
plt.subplot(335),plt.imshow(lap1),plt.title('lap 2 order Derivative')
plt.xticks([]), plt.yticks([])
plt.subplot(336),plt.imshow(sharp2),plt.title('lap only 1 Derivative')
plt.xticks([]), plt.yticks([])
plt.subplot(337),plt.imshow(sob1),plt.title('sob1 in x')
plt.xticks([]), plt.yticks([])
plt.subplot(338),plt.imshow(sob2),plt.title('sob2 in y')
plt.xticks([]), plt.yticks([])
plt.show()

convolution operation on an image:

高斯模糊

lap锐化：

Ref