dataStructure_BinaryIndexedTree - 二叉索引树（树状数组）

Posted on 2021-12-15 Edited on 2023-08-03

BITree 详解

1 Binary Indexed Tree(二元索引树)(树状数组)

1 用途：以O(log n)时间复杂度得到任意区间和。同时支持在O(log n)时间内支持动态单点值的修改。空间复杂度O(n)。
2 出处：Peter M. Fenwick. A new data structure for cumulative frequency tables. Software: Practice and Experience. 1994, 24 (3): 327–336. doi:10.1002/spe.4380240306.

3 原理：按照Peter M. Fenwick的说法，正如所有的整数都可以表示成2的幂和，我们也可以把一串序列表示成一系列子序列的和。采用这个想法，我们可将一个前缀和划分成多个子序列的和，而划分的方法与数的2的幂和具有极其相似的方式。一方面，子序列的个数是其二进制表示中1的个数，另一方面，子序列代表的f[i]的个数也是2的幂。
如下说明也很贴切：

1
2

How does Binary Indexed Tree work? 
The idea is based on the fact that all positive integers can be represented as the sum of powers of 2. For example 19 can be represented as 16 + 2 + 1. Every node of the BITree stores the sum of n elements where n is a power of 2. For example, in the first diagram above (the diagram for getSum()), the sum of the first 12 elements can be obtained by the sum of the last 4 elements (from 9 to 12) plus the sum of 8 elements (from 1 to 8). The number of set bits in the binary representation of a number n is O(Logn). Therefore, we traverse at-most O(Logn) nodes in both getSum() and update() operations. The time complexity of the construction is O(nLogn) as it calls update() for all n elements.

2 直观解释

1 C[i]表示f[1]…f[i]的和，而用tree[idx]表示某些子序列的和
2 实际上tree[idx]是那些indexes from (idx - 2^r + 1) to idx的f[index]的和,其中r是idx最右边的那个非零位到右边末尾的0的个数，比如：
- eg 2.0 当idx=8 decimal = 1000,有r=3，则，tree[8] = f[1] + … + f[8],
- eg 2.1 当idx=11 decimal = 1011,有r=0，则，tree[11] = f[11],
- eg 2.2 当idx=12 decimal = 1100,有r=2，则，tree[12] = f[9] + f[10] + f[11] + f[12],
- eg 2.3 当idx=14 decimal = 1110,有r=1，则，tree[14] = f[13] + f[14]
3 有了上面tree这个数组(也就是bit本体)，我们可以得到： C[13] = tree[13] + tree[12] + tree[8]
- 从上述例子可以得出一个重要结论：求前idx个和，也就是求C[idx]的时候，idx中1的个数即为构成C[idx]的子序列的个数，也就是有多少个tree中的元素加起来
  
  C1 = f1
  
  C2 = f1 + f2
  
  C3 = f3
  
  C4 = f1 + f2 + f3 + f4
  
  C5 = f5
  
  C6 = f5 + f6
  
  C7 = f7
  
  C8 = f1 + f2 + f3 + f4 + f5 + f6 + f7 + f8
  
  …
  
  C16 = f1 + f2 + f3 + f4 + f5 + f6 + f7 + f8 + f9 + f10 + f11 + f12 + f13 + f14 + f15 + f16

4 有了3作为基础，求前缀和过程如下：4,5参考

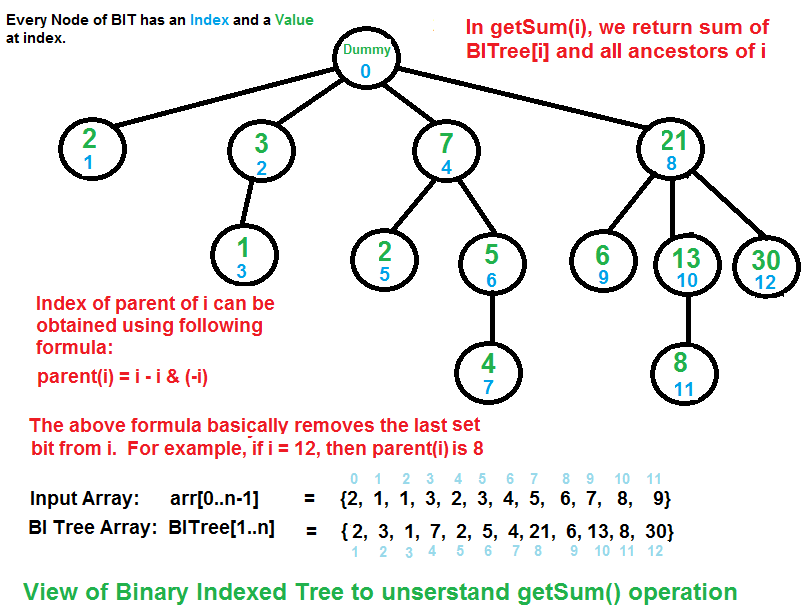
https://cdn.jsdelivr.net/gh/xychen5/blogImgs@main/imgs/BITSum.3uh1v2dddp40.png

4.1 tree[y] 是 tree[x] 的父节点，当且仅当可以通过从 x 的二进制表示中去除最后一个设置位(即数位为1的位)来获得 y，即 y = x – (x & (-x))。
- lowbit函数就是取最后一个设置位的函数，lowbit = [](int x) int {return (x & (-x));}
- eg: tree[8]是tree[10]的父节点，因为 10 - (10&(-10)) == 8 为true
4.2 节点 tree[y] 的子节点 tree[x] 存储了 y(inclusive) 和 x(exclusive) 之间元素的总和：arr[y,…,x)。

4.3 实际例子：求C[11] = C[1011]：

4.3.1 看下图即可，很显然我们需要沿着路径一直加到dummy node(tree[0]其值为0，方便运算而已)为止，从这里能够再一次看出，为何其前缀和的算法时间复杂度为O(log n)，因为路径上的node个数就是C[1011]中的1的个数
C[1011] = C[11] = tree[11] + tree[10] + tree[8]

4.3.2具体代码：

int getSum(int BITree[], int index)
{
    int sum = 0; // Initialize result
    // index in BITree[] is 1 more than the index in arr[]
    index = index + 1;
    // Traverse ancestors of BITree[index]
    while (index>0)
    {
        // Add current element of BITree to sum
        sum += BITree[index];
        // Move index to parent node in getSum View
        index -= index & (-index);
    }
    return sum;
}

5 更新BITree

5.1 类似4中的求和，更改一个节点需要更改所有被当前节点所影响的子节点
5.2 子节点的获取： parent of idx = idx + (idx & (-idx));

5.3 举个例子，如4中的图：对于idx = 2这个点，需要更新节点4,8

void updateBIT(int BITree[], int n, int index, int val)
{
    // index in BITree[] is 1 more than the index in arr[]
    index = index + 1;
    // Traverse all ancestors and add 'val'
    while (index <= n)
    {
        // Add 'val' to current node of BI Tree
        BITree[index] += val;
        // Update index to that of parent in update View
        index += index & (-index);
    }
}

3 整体实现

// C++ code to demonstrate operations of Binary Index Tree
#include <iostream>

using namespace std;

/*		 n --> No. of elements present in input array.
	BITree[0..n] --> Array that represents Binary Indexed Tree.
	arr[0..n-1] --> Input array for which prefix sum is evaluated. */

// Returns sum of arr[0..index]. This function assumes
// that the array is preprocessed and partial sums of
// array elements are stored in BITree[].
int getSum(int BITree[], int index)
{
	int sum = 0; // Initialize result

	// index in BITree[] is 1 more than the index in arr[]
	index = index + 1;

	// Traverse ancestors of BITree[index]
	while (index>0)
	{
		// Add current element of BITree to sum
		sum += BITree[index];

		// Move index to parent node in getSum View
		index -= index & (-index);
	}
	return sum;
}

// Updates a node in Binary Index Tree (BITree) at given index
// in BITree. The given value 'val' is added to BITree[i] and
// all of its ancestors in tree.
void updateBIT(int BITree[], int n, int index, int val)
{
	// index in BITree[] is 1 more than the index in arr[]
	index = index + 1;

	// Traverse all ancestors and add 'val'
	while (index <= n)
	{
	// Add 'val' to current node of BI Tree
	BITree[index] += val;

	// Update index to that of parent in update View
	index += index & (-index);
	}
}

// Constructs and returns a Binary Indexed Tree for given
// array of size n.
int *constructBITree(int arr[], int n)
{
	// Create and initialize BITree[] as 0
	int *BITree = new int[n+1];
	for (int i=1; i<=n; i++)
		BITree[i] = 0;

	// Store the actual values in BITree[] using update()
	for (int i=0; i<n; i++)
		updateBIT(BITree, n, i, arr[i]);

	// Uncomment below lines to see contents of BITree[]
	//for (int i=1; i<=n; i++)
	//	 cout << BITree[i] << " ";

	return BITree;
}


// Driver program to test above functions
int main()
{
	int freq[] = {2, 1, 1, 3, 2, 3, 4, 5, 6, 7, 8, 9};
	int n = sizeof(freq)/sizeof(freq[0]);
	int *BITree = constructBITree(freq, n);
	cout << "Sum of elements in arr[0..5] is "
		<< getSum(BITree, 5);

	// Let use test the update operation
	freq[3] += 6;
	updateBIT(BITree, n, 3, 6); //Update BIT for above change in arr[]

	cout << "\nSum of elements in arr[0..5] after update is "
		<< getSum(BITree, 5);

	return 0;
}

实际例题

剑指 Offer 51. 数组中的逆序对

1 题目

https://leetcode-cn.com/problems/shu-zu-zhong-de-ni-xu-dui-lcof/

2 解题思路

1 思路：
- 1.1 首先注意到：对于数组{5，5,2,3,6}而言，得到每个value的个数的统计：
  - index -> 1 2 3 4 5 6 7 8 9
  - value -> 0 1 1 0 2 1 0 0 0
- 1.2 那么上述过程中，比如对于5，其贡献的逆序数对为5之前所有数字出现次数的和，也就是value数组中2之前的前缀和！
2 那么如何快速获得前缀和呢？考虑使用BST来获取，参考:
- 2.1 整体思路如下：
  - a 使用数字在数组中的排名来代替数字（这不会对逆序数对的个数产生影响）
  - b 对数组nums中的元素nums[i]从右到左构建BITree（i 从 n-1 到 0），注意，BITree所对应的前缀和是数组里数字出现次数的和
    - 比如进行到nums[i]，那么nums[i]右边的数字都已经统计了他们的出现次数，而后获取nums[i] - 1的前缀和，即可获取所有 < nums[i]的数字在nums[i:n]中的出现次数之和，也就是nums[i]贡献的逆序数对的个数
    - 之所以是逆序遍历构建BITree，是因为对于nums[i]，它能够贡献的逆序数对的个数仅仅出现在它的右侧，所以需要在右侧进行
- 2.2 额外说一下数组离散化，也就是不关系数字大小本身，只关心他们之间的相对排位
  1
  2
  3
  4
  5
  sort(sortNoNums.begin(), sortNoNums.end(), std::less<int>());
  
  for(auto& num : nums) {
  num = lower_bound(sortNoNums.begin(), sortNoNums.end(), num) - sortNoNums.begin() + 1;
  }
  相似题目：
  https://leetcode-cn.com/problems/count-of-smaller-numbers-after-self/

class Solution {
public:
    class BIT {
    public: 
        vector<int> tree;
        int n;
        BIT(int _n): n(_n) , tree(_n + 1){cout << "init Done!" << endl;};

        // find prefixSum with index x
        int query(int x) {
            int sum = 0;
            while(x > 0) {
                sum += tree[x];
                x -= (x&(-x));
            }
            return sum;
        }

        // update x with delta val v
        void update(int x, int v) {
            cout << "d1"<< endl;
            while(x <= n) {
                tree[x] += v;
                x += (x&(-x));
            }
            cout << "d2"<< endl;
        }
    };

    int reversePairs(vector<int>& nums) {
        // desrialization, using sort no to denote the value
        vector<int> sortNoNums = nums;
        sort(sortNoNums.begin(), sortNoNums.end(), std::less<int>());
        
        for(auto& num : nums) {
            num = lower_bound(sortNoNums.begin(), sortNoNums.end(), num) - sortNoNums.begin() + 1;
        }

        // using binary indexed tree to statistic the reversePair num
        // start from the end of nums, so that the prefix in BIT means the reversePiar num
        int ans = 0;
        BIT bit(nums.size());
        for(int i = nums.size() - 1; i >= 0; --i) {
            ans += bit.query(nums[i] - 1); // cause only elements right than current num[i] will contribute to the ans
            cout << ans << endl;
            // statistic frequence of nums[i]
            bit.update(nums[i], 1);
        }

        return ans;
    }
};

0315. 计算右侧小于当前元素的个数

1 题目

https://leetcode-cn.com/problems/count-of-smaller-numbers-after-self/

题和逆序数对的计算方式相同：https://leetcode-cn.com/problems/shu-zu-zhong-de-ni-xu-dui-lcof/

2 解题思路

1 思路：
- 1.1 首先注意到：对于数组{5，5,2,3,6}而言，得到每个value的个数的统计：
  - index -> 1 2 3 4 5 6 7 8 9
  - value -> 0 1 1 0 2 1 0 0 0
- 1.2 那么上述过程中，比如对于5，其贡献的逆序数对为5之前所有数字出现次数的和，也就是value数组中2之前的前缀和！
2 那么如何快速获得前缀和呢？考虑使用BST来获取，参考:https://xychen5.github.io/2021/12/15/dataStructure-BinaryIndexedTree/
- 2.1 整体思路如下：
  - a 使用数字在数组中的排名来代替数字（这不会对逆序数对的个数产生影响）
  - b 对数组nums中的元素nums[i]从右到左构建BITree（i 从 n-1 到 0），注意，BITree所对应的前缀和是数组里数字出现次数的和
    - 比如进行到nums[i]，那么nums[i]右边的数字都已经统计了他们的出现次数，而后获取nums[i] - 1的前缀和，即可获取所有 < nums[i]的数字在nums[i:n]中的出现次数之和，也就是nums[i]贡献的逆序数对的个数
    - 之所以是逆序遍历构建BITree，是因为对于nums[i]，它能够贡献的逆序数对的个数仅仅出现在它的右侧，所以需要在右侧进行
- 2.2 额外说一下数组离散化，也就是不关系数字大小本身，只关心他们之间的相对排位
  1
  2
  3
  4
  5
  sort(sortNoNums.begin(), sortNoNums.end(), std::less<int>());
  
  for(auto& num : nums) {
  num = lower_bound(sortNoNums.begin(), sortNoNums.end(), num) - sortNoNums.begin() + 1;
  }
  如下的过程并没有使用离散化，但是空间浪费也不是很多，超过百分之83吧

class Solution {
public:
    class BIT {
    public: 
        vector<int> tree;
        int n;
        BIT(int _n): n(_n) , tree(_n + 1){cout << "init Done!" << endl;};

        // find prefixSum with index x
        int query(int x) {
            int sum = 0;
            while(x > 0) {
                sum += tree[x];
                x -= (x&(-x));
            }
            return sum;
        }

        // update x with delta val v
        void update(int x, int v) {
            cout << "d1"<< endl;
            while(x <= n) {
                tree[x] += v;
                x += (x&(-x));
            }
            cout << "d2"<< endl;
        }
    };

    int reversePairs(vector<int>& nums) {
        // desrialization, using sort no to denote the value
        vector<int> sortNoNums = nums;
        sort(sortNoNums.begin(), sortNoNums.end(), std::less<int>());
        
        for(auto& num : nums) {
            num = lower_bound(sortNoNums.begin(), sortNoNums.end(), num) - sortNoNums.begin() + 1;
        }

        // using binary indexed tree to statistic the reversePair num
        // start from the end of nums, so that the prefix in BIT means the reversePiar num
        int ans = 0;
        BIT bit(nums.size());
        for(int i = nums.size() - 1; i >= 0; --i) {
            ans += bit.query(nums[i] - 1); // cause only elements right than current num[i] will contribute to the ans
            cout << ans << endl;
            // statistic frequence of nums[i]
            bit.update(nums[i], 1);
        }

        return ans;
    }
};

0327. 区间和的个数

1 题目

https://leetcode-cn.com/problems/count-of-range-sum/

题和逆序数对的计算方式相同：https://leetcode-cn.com/problems/shu-zu-zhong-de-ni-xu-dui-lcof/
就是做了一个小改变而已，很多统计区间值的，st-ed < tar, 本来是让你找一个st，ed的对子的，那么就会转换思路为：
对于每一个ed找st，什么样的呢？ st < ed + tar
然后找这样的st就有很多方法，比如hash，前缀和，bitree，priority_queue

2 解题思路

1 求逆序对的思路：
- 1.1 首先注意到：对于数组{5，5,2,3,6}而言，得到每个value的个数的统计：
  - index -> 1 2 3 4 5 6 7 8 9
  - value -> 0 1 1 0 2 1 0 0 0
- 1.2 那么上述过程中，比如对于5，其贡献的逆序数对为5之前所有数字出现次数的和，也就是value数组中2之前的前缀和！
2 那么如何快速获得前缀和呢？考虑使用BST来获取，参考:https://xychen5.github.io/2021/12/15/dataStructure-BinaryIndexedTree/
- 2.1 整体思路如下：
  - a 使用数字在数组中的排名来代替数字（这不会对逆序数对的个数产生影响）
  - b 对数组nums中的元素nums[i]从右到左构建BITree（i 从 n-1 到 0），注意，BITree所对应的前缀和是数组里数字出现次数的和
    - 比如进行到nums[i]，那么nums[i]右边的数字都已经统计了他们的出现次数，而后获取nums[i] - 1的前缀和，即可获取所有 < nums[i]的数字在nums[i:n]中的出现次数之和，也就是nums[i]贡献的逆序数对的个数
    - 之所以是逆序遍历构建BITree，是因为对于nums[i]，它能够贡献的逆序数对的个数仅仅出现在它的右侧，所以需要在右侧进行
- 2.2 额外说一下数组离散化，也就是不关系数字大小本身，只关心他们之间的相对排位

3 那么小改变在哪里呢？

就是查一次查不出来了，要查两次做一个差

还有一点就是，注意将所有要query和update的值，都用序号表示，这样避免tree过大

1
2
3

for a valid s(i, j) we shall find:
     preSum[j] - ub <= preSum[i] <= preSum[j] - lb
we just need to statistic those preSum[i] for each j

实现代码如下：

class Solution {
public:
    // when count the num, try to use BItree to count the appeared num, prefixSum to 
    // get how many < curNum will be fast
    class BITree{
    public:
        int n;
        vector<int> tree;
        BITree (int _n) : n(_n), tree(_n + 1) {}

        int lowBit(int x) {
            return x & (-x);
        }

        int query(int x) {
            int sum = 0;
            while(x > 0) {
                sum += tree[x];
                x -= lowBit(x);
            }
            return sum;
        }

        void update(int x, int val) {
            while(x <= n) {
                // cout << "x and tree[x] " << x << "->" << tree[x] << endl;
                tree[x] += val;
                x += lowBit(x);
            }
        }
    };


    int countRangeSum(vector<int>& nums, int lower, int upper) {
        unordered_map<int, int> numToIdx;
        set<long long> tmpNums;
        vector<long long> prefixSum = {0};

        for(int i = 0; i < nums.size(); ++i) {
            prefixSum.emplace_back(nums[i] + prefixSum.back());
        }

        for(auto ps : prefixSum) {
            tmpNums.insert(ps);
            tmpNums.insert(ps - lower);
            tmpNums.insert(ps - upper);
        }
        
        int i = 1;
        for(auto num : tmpNums) {
            numToIdx[num] = i++;
        }

        // for a valid s(i, j) we shall find:
        //     preSum[j] - ub <= preSum[i] <= preSum[j] - lb
        // we just need to statistic those preSum[i] for each j
        int n = tmpNums.size();
        BITree tree(n + 1);
        long long ans = 0;
        for(int j = 0; j < prefixSum.size(); ++j) {
            int leftBound = numToIdx[prefixSum[j] - upper];
            int rightBound = numToIdx[prefixSum[j] - lower];
            // cout << "lb, rb = " << leftBound << " " << rightBound << endl;
            ans += (tree.query(rightBound) - tree.query(leftBound - 1));
            // cout << "ans = " << ans << "preFixSumSize = " << prefixSum.size() << endl;
            tree.update(numToIdx[prefixSum[j]], 1); // avoid 0 to produce dead loop
        }
        return ans;
    }
};

3 使用线段树解题

注意其中很重要的一点：
对于线段树中插入一个节点时，需要对沿路所有节点的sum加上要插入的节点的值，找这个节点位置的时候，
需要找到root左右管辖范围的中间值mid，此时务必使用>>1去做，因为获得mid我们要求其为 floor(left + right),
但是：(cpp和python对于移位和除法的逻辑是相同的)，这里就显示出了2者的区别，
当然在数字都为正数的时候不会出错！

>>> int((-1 + 0) / 2)
0
>>> int((-1 + 0)  >> 1)
-1

class Solution {
public:
    class SegTree {
    public:
        struct SegNode {
            long long  leftBound = 0, rightBound = 0, curSum = 0;
            SegNode* lChild = nullptr;
            SegNode* rChild = nullptr;
            SegNode(long long lb, long long rb) :
                leftBound(lb),
                rightBound(rb),
                curSum(0),
                lChild(nullptr),
                rChild(nullptr) {
            }
        };

        SegNode* root;


        SegTree(long long  left, long long  right) {
            root = build(left, right);
        }

        SegTree() {}

        SegNode* build(long long  l, long long  r) {
            SegNode* node = new SegNode(l, r);
            if(l == r) {
                return node;
            }

            long long  mid = (l + r) / 2;
            node->lChild = build(l, mid);
            node->rChild = build(mid + 1, r);
            return node;
        }

        void insert(SegNode* root, long long  tarIdx, long long  val) {
            root->curSum += val; 
            if(root->leftBound == root->rightBound) {
                return;
            }
            long long  mid = (root->leftBound + root->rightBound) >> 1;
            // long long  mid = (root->leftBound + root->rightBound) / 2;
            // there are identicial difference between them two:
            // eg: when left == -1, right = 0;
            //     case1 => (left + right) / 2 == 0
            //     case1 => (left + right) >> 1 == -1
            // cout << "d1 " << tarIdx << " mid: " << mid << " root:l/r: " << root->leftBound << "/" << root->rightBound << endl;
            if(tarIdx <= mid) {
            // cout << "d2" << endl;
                if (nullptr == root->lChild) {
                    // cout << "d2.5" << endl;
                    root->lChild = new SegNode(root->leftBound, mid);
                }
                insert(root->lChild, tarIdx, val);
            }
            else{
            // cout << "d3" << endl;
                if (nullptr == root->rChild) {
                    root->rChild = new SegNode(mid + 1, root->rightBound);
                }
                insert(root->rChild, tarIdx, val);
            }
        }

        long long  getSum(SegNode* root, long long  left, long long  right) const {
            if(nullptr == root) {
                return 0;
            }
            // 当前节点位于目标区间外
            if(left > root->rightBound || right < root->leftBound) {
                return 0;
            }
            // 当前节点位于目标区间内
            if(left <= root->leftBound && right >= root->rightBound) {
                // cout << "left/right" << left << "/" << right << " => " << root->curSum << endl;
                return root->curSum;
            }
            return getSum(root->lChild, left, right) + getSum(root->rChild, left, right);
        }

    };

    int countRangeSum(vector<int>& nums, int lower, int upper) {
        unordered_map<int, int> numToIdx;
        set<long long> tmpNums;
        vector<long long> prefixSum = {0};

        for(int i = 0; i < nums.size(); ++i) {
            prefixSum.emplace_back(nums[i] + prefixSum.back());
        }

        for(auto ps : prefixSum) {
            tmpNums.insert(ps);
            tmpNums.insert(ps - lower);
            tmpNums.insert(ps - upper);
        }
        
        int i = 1;
        for(auto num : tmpNums) {
            numToIdx[num] = i++;
        }

        // for a valid s(i, j) we shall find:
        //     preSum[j] - ub <= preSum[i] <= preSum[j] - lb
        // we just need to statistic those preSum[i] for each j
        int n = tmpNums.size();
        // BITree tree(n + 1);
        long long ans = 0;
        // for(int j = 0; j < prefixSum.size(); ++j) {
        //     int leftBound = numToIdx[prefixSum[j] - upper];
        //     int rightBound = numToIdx[prefixSum[j] - lower];
        //     // cout << "lb, rb = " << leftBound << " " << rightBound << endl;
        //     ans += (tree.query(rightBound) - tree.query(leftBound - 1));
        //     // cout << "ans = " << ans << "preFixSumSize = " << prefixSum.size() << endl;
        //     tree.update(numToIdx[prefixSum[j]], 1); // avoid 0 to produce dead loop
        // }
        
        // try to use segnode tree to sovle the problem, this will exceed the time limitation
        // SegTree tree(0, n + 1);
        // for(int j = 0; j < prefixSum.size(); ++j) {
        //     int left = numToIdx[prefixSum[j] - upper];
        //     int right = numToIdx[prefixSum[j] - lower];
        //     ans += tree.getSum(tree.root, left, right);
        //     // cout << "lb, rb = " << left<< " " << right<< " ==> " << ans << endl;
        //     tree.insert(tree.root, numToIdx[prefixSum[j]], 1);
        //     // cout << "insert: " << numToIdx[prefixSum[j]]  << "curRoot: " << tree.root->curSum << endl;
        // }

        // we do not do the deserialization
        long long minLeft = LLONG_MAX, maxRight = LLONG_MIN;
        for(long long x : prefixSum) {
            minLeft = min({minLeft, x, x - lower, x - upper});
            maxRight = max({maxRight, x, x - lower, x - upper});
        }
        
        // cout << "minL, maxR" << minLeft << " " << maxRight <<endl; 
        SegTree tree;
        tree.root = new SegTree::SegNode(minLeft, maxRight);
        // reason why we insert the prefixSum of 0, because for the first ele:
        // if it statisfy the interval, then it will be statisticed because the 0
        for(long long x : prefixSum) {
            ans += tree.getSum(tree.root, x - upper, x - lower);
            // cout << "lb, rb = " << x - upper<< " " << x - lower << " ==> ans = " << ans << endl;
            tree.insert(tree.root, x, 1);
            // cout << "insert: " <<  x << "curRoot: " << tree.root->curSum << endl;
        }

        return ans;
    }
}

0493 翻转对

1 题目

https://leetcode-cn.com/problems/reverse-pairs/

2 解题思路

1 求逆序对的思路：
- 1.1 首先注意到：对于数组{5，5,2,3,6}而言，得到每个value的个数的统计：
  - index -> 1 2 3 4 5 6 7 8 9
  - value -> 0 1 1 0 2 1 0 0 0
- 1.2 那么上述过程中，比如对于5，其贡献的逆序数对为5之前所有数字出现次数的和，也就是value数组中2之前的前缀和！
2 那么如何快速获得前缀和呢？考虑使用BST来获取，参考:https://xychen5.github.io/2021/12/15/dataStructure-BinaryIndexedTree/
- 2.1 整体思路如下：
  - a 使用数字在数组中的排名来代替数字（这不会对逆序数对的个数产生影响）
  - b 对数组nums中的元素nums[i]从右到左构建BITree（i 从 n-1 到 0），注意，BITree所对应的前缀和是数组里数字出现次数的和
    - 比如进行到nums[i]，那么nums[i]右边的数字都已经统计了他们的出现次数，而后获取nums[i] - 1的前缀和，即可获取所有 < nums[i]的数字在nums[i:n]中的出现次数之和，也就是nums[i]贡献的逆序数对的个数
    - 之所以是逆序遍历构建BITree，是因为对于nums[i]，它能够贡献的逆序数对的个数仅仅出现在它的右侧，所以需要在右侧进行
- 2.2 额外说一下数组离散化，也就是不关系数字大小本身，只关心他们之间的相对排位
3 那么小改变在哪里呢？
- 对于每个j，找位于它之前的数字，满足：nums[i] > 2*nums[j]
- 找的方法为用总体减去目标的补集：用nums[j]之前所有的数字的个数，减去小于等于nums[j] * 2的数字就行
  
  for each j, find those nums[i]:
  which satisty: i < j && nums[i] > 2*nums[j]
  
  so, we can get this by: using all to sub those nums[i] <= nums[j] * 2 to get the res
  preSum[1 -> 2*n] - preSum[1 -> 2*nums[j]]

实现代码如下：

class Solution {
public:

    class BITree {
    public:
        long long n;
        vector<long long> tree;
        BITree(long long _n) : n(_n), tree(_n + 1) {}
        
        long long lowBit(long long x) {
            return x & (-x);
        }

        long long query(long long x) {
            long long sum = 0;
            while(x > 0) {
                sum += tree[x];
                x -= lowBit(x);
            }
            return sum;
        }

        void update(long long x, long long val) {
            while(x <= n) {
                tree[x] += val;
                x += lowBit(x);
            }
        }
    };

    int reversePairs(vector<int>& nums) {
        // deserialization
        vector<long long> tmpNums;
        for(auto num : nums) {
            tmpNums.emplace_back(num);
            tmpNums.emplace_back(num * 2LL);
        }
        sort(tmpNums.begin(), tmpNums.end(), [](long a, long b) {
            return a < b;
        });

        // for(auto& num : tmpNums) { cout << "tmp: " << num << endl;}
        
        // for(auto& num : nums) {
        //     num = lower_bound(tmpNums.begin(), tmpNums.end(), num) - tmpNums.begin() + 1; //  +1 to avoid update(0, 1) failure
        // }

        for(auto& num : nums) { cout << "num No: " << num << endl;}

        // deserialization
        int idx = 1;
        unordered_map<long long,long long> numToIdx;
        for(auto num : tmpNums) {
            numToIdx[num] = idx ++;
        }

        int n = nums.size();
        int ans = 0;
        BITree tree(2 * n);
        // for each j, find those nums[i]:
        // which satisty: i < j && nums[i] > 2*nums[j]
        // 
        // so, we can get this by: using all to sub those nums[i] <= nums[j] * 2 to get the res
        // preSum[1 -> 2*n] - preSum[1 -> 2*nums[j]]
        for(int i = 0; i < n; ++i) {
            // cout << "counting: " << nums[i] << endl;
            // attention the diff between 2LL and 2
            ans += (tree.query( 2LL*n ) - tree.query(numToIdx[2LL * nums[i]]));
            tree.update(numToIdx[nums[i]], 1);
        }

        return ans;
    }
}

lcBinarySearchTreeAndRecursiveWay

Posted on 2021-12-14 Edited on 2023-08-03

0 递归和bst

1 构建bst 0108. 将有序数组转换为二叉搜索树

1 题目

https://leetcode-cn.com/problems/convert-sorted-array-to-binary-search-tree/

2 解题思路

1 AVL tree最主要的特性在于，任何子树的左子树和右子树的高度差不超过1，所以方法为：

1.1 每次找到数组中间的值作为root，然后两边分别作为左右子树，左边都比root小，右边都大，刚好满足AVL要求

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        // find root whose left size and right size shall equal
        int n = nums.size();
        if(n <= 0) {
            return nullptr;
        }
        vector<int> left(nums.begin(), nums.begin() + n / 2);
        vector<int> right(nums.begin() + n / 2 + 1, nums.end());
        TreeNode* root = new TreeNode(
            nums[n/2]
            sortedArrayToBST(left),
            sortedArrayToBST(right)
        );
        return root;
    }
};

2 select k from n: C(n, k)

void selectKFromN(int st, int k, vector<vector<int>>& res, vector<int>& nums, vector<int>& tmpRes) {
    if(k == 0) {
        res.emplace_back(tmpRes);
        return;
    }
    for(int i = st; i < nums.size() - k + 1; ++i) {
        tmpRes.emplace_back(nums[i]);
        selectKFromN(i + 1, k - 1, res, nums, tmpRes);
        tmpRes.pop_back();
    }
}

1 递归

0025 最大因数联通分量大小

1 题目

https://leetcode-cn.com/problems/reverse-nodes-in-k-group/

2 解题思路

1 个人思路：
- 首先很明显能够发现子问题的痕迹，子问题就是翻转长度为k的链表
- 翻转用长度为k的栈去模拟即可
2 优化：使用常数空间：
- 使用三个指针，a->b->c的链表的话，那么就是说(三个指针相当于滑动窗口的感觉)：
- 记录下a,b,c的指针，然后把a<-b<-c,然后移动这三个指针即可

/** 
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        // return headK -> reverse(afterHeadK, k);
        return reverse(head, k);
    }

    ListNode* reverse(ListNode* head, int k ) {
        ListNode* tmp = head;
        vector<ListNode*> vec = {};
        for(int i = 0; i < k; ++i) {
            if(tmp != nullptr) {
                vec.emplace_back(tmp);
                tmp = tmp -> next;
            }
        }

        if(vec.size() != k) {
            return head;
        }

        ListNode* nextHead = vec.back()->next;

        for(int i = k-1; i >= 1; --i) {
            // cout << i << "**" << endl;
            vec[i]->next = vec[i-1];
            // cout << vec[i]->val << " -> " << vec[i-1]->val << endl;
        }
        vec[0]->next = reverse(nextHead, k);
        
        // cout << "asdf**" << endl;
        return vec.back();
    }
};

1.1

0761 makeLargestSpecial 特殊的二进制序列

1 题目

https://leetcode-cn.com/problems/special-binary-string

2 解题思路

1 个人思路：

首先这个特殊子序列，采用合理的括号串去理解特殊子序列就好了
然后大致的递归思路：
- 1.1 首先找到原来串里所有特殊的子序列
- 1.2 将这些子序列按照字典序排序
- 1.3 排序后加起来得到结果
- 1.4 eg： 10 1100 111000，这个串可以分成三个特殊子序列：那么最大字典序显然就是 111000 1100 10
上面的还有其他问题，若子串一开始不能分为特殊子序列呢？
- eg：1 10 1100 0，那么首先剥去外壳，然后再递归进去，对10 1100采用上述子序列方法
递归返回？当子序列长度小于等于2，就直接返回字符串北盛即可

有个很容易出错误的示例需要注意：

we shall reArrange first and then sort,
because when we reArrage, we my produce bigger subStr,
if we sort first and reArrange all subpart we could get false res: eg:
input: “11100011010101100100”
false Result: “111000 11100101010100” // part2 is bigger subStr, so we shall reArrange all sub first and then sort
std result: “11100101010100 111000”

class Solution {
public:
    string makeLargestSpecial(string s) {
        string res = reArrange(s);
        // string lastRes = "";
        // while(res != reArrange(res)){
        //     res = reArrange(res);
        // };
        return res;
    }

    string reArrange(string s) {
        // cout << "c1->"  << s << endl;
        int n = s.size();
        if(s.size() <= 2) {
            // cout << "less than 2: " << s << endl;
            return s;
        }

        // firstly, get all special subStr and sort as the lexical order
        vector<string> subStr;

        int st = 0;
        int cntRedundantNumberOne = 1;
        for(int i = st + 1; i < n; ++i) {
            cntRedundantNumberOne += (s[i] == '1' ? 1 : -1);
            if(0 == cntRedundantNumberOne) {
                subStr.emplace_back(s.substr(st, i - st + 1));
                st = i + 1;
                cntRedundantNumberOne = 0;
            }
        }

        if(1 == subStr.size()) {

            return s.substr(0, 1) + reArrange(s.substr(1, n-2)) + s.substr(n-2, 1);
        }

        // for(auto i : subStr) {
        //     cout << i << endl;
        // }
        
        
        // secondly, sort all sub part and sum up
        // cout << "a" << endl;
        for(int i = 0; i < subStr.size(); ++i) {
            subStr[i] = reArrange(subStr[i]);
        }
        // we shall reArrange first and then sort,
        // because when we reArrage, we my produce bigger subStr, 
        // if we sort first and reArrange all subpart we could get false res: eg: 
        // input:        "11100011010101100100"
        // false Result: "111000 11100101010100" // part2 is bigger subStr, so we shall reArrange all sub first and then sort
        // std result:   "11100101010100 111000" 
        sort(subStr.begin(), subStr.end(), std::greater<string>());

        string res = "";
        for(auto s : subStr) {
            res += s;
        }

        // cout << "c2" << endl;
        return res;
    }
};

0010 isMatch 正则表达式匹配

1 题目

https://leetcode-cn.com/problems/regular-expression-matching

2 解题思路

0 心得：
- 递归适用于减小规模后问题的处理方式不会发生改变的场景
- 对于递归，得明白当层递归处理会如何将问题规模减小
1 个人思路：
- 首先这个字符串匹配，需要理解每一次能够用p去匹配什么？然后怎么匹配
- 1.1 首先每次递归，p的规模减小肯定是在p的头部：对于p的匹配类型，有3种：
  - 1.1.1 s = ab, p = ab, 那么就用p的第一个字母去匹配
  - 1.1.2 s = a, p = ., 同样需要用p的第一个字幕去匹配
  - 1.1.3 带*的，这个需要将p的头两个拿去和s匹配：
    - s = a, p1 = .*, p2 = a*,这两种情况，都是满足需要的
    - s = a, p1 = c*.*，那么第一个c*是不匹配的，同样的还有.*是否需要匹配的问题
- 然后大致的递归思路：
  - 1.1 首先从p的头部分析是哪种子模式
  - 1.2 按照该种子模式匹配
  - 1.3 递归到下层的p和s，这样p和s都因为1.1~1.2的过程中变小了，完成了使用递归解决问题的思路
- 递归返回？
  - 1.1 s的长度为0？
  - 1.2 p的长度为0？
- 对于上述过程不清楚的请以下面两个结果作为例子：
  1
  2
  3
  4
  5
  6
  7
  "bcabac"
  "a*a*.*b*b*"
  return: true
  
  "a"
  ".*..a*"
  return false

class Solution {
public:
    bool isMatch(string s, string p) {
        return greadyMatch(s, p);
    }

    bool greadyMatch(string s, string p) {
        int sLen = s.size();
        int pLen = p.size();
        // cout << "sLen & pLen => " << sLen << " " << pLen << s << " " << p << endl;
        if(pLen == 2 && p[0] == '.' && p[1] == '*') {
            return true;
        }

        if(pLen == 1) {
            if(sLen != 1) {
                return false;
            }
            return p[0] == '.' ? true : p[0] == s[0];
        }
        
        if(sLen == 0) {
            if(pLen == 0) {
                return true;
            }
            if(pLen == 2) {
                if(p[1] == '*') {
                    return true;
                }else {
                    return false;
                }
            } else {
                if(p[1] == '*') {
                    return greadyMatch(s, p.substr(2));
                } else {
                    return false;
                }
            }
        }

        if(pLen == 0) {
            return sLen == 0;
        }

        // match as much as possible
        char head0 = p[0];
        char head1 = p[1];
        bool res = false;

        if(p[0] == '.') {
            if(p[1] == '*') {
                // match any len >= 1 of s, when len == 0, then not match
                for(int len = 0; len <= sLen; ++len) {
                    res = res || greadyMatch(s.substr(len), p.substr(2));
                    // cout << "tried: " << s.substr(len) << " " << p.substr(2) << endl;
                }
                return res;
            } else { 
                return greadyMatch(s.substr(1), p.substr(1));
            }
        } else {
            // p[0] = a~z
            if(p[0] != s[0]) {
                if(p[1] == '*') {
                    // cout << p.substr(2) << "\nculled!" <<endl;
                    return greadyMatch(s, p.substr(2));
                } else {
                    return false;
                }
            } else {

                if(p[1] == '*') {
                    int sameLen = s.find_first_not_of(p[0]);
                    if(sameLen == -1) {
                        sameLen = sLen;
                    }
                    // cout << "sameLen2 -> " << sameLen << s.substr(1) << p.substr(2) << endl;
                    // when len = 0, not use this * to match
                    for(int len = 0; len <= sameLen; ++len) {
                        res = res || greadyMatch(s.substr(len), p.substr(2));
                    }
                    return res;
                } else {
                    return greadyMatch(s.substr(1), p.substr(1));
                }
            }
            
        }
        
        // never be executed
        return res;
    }
};

2 二叉搜索树(平衡意味着任意两个子树高度差不应该大于1)

1373 maxSumBST 二叉搜索子树的最大键值和

1 题目

https://leetcode-cn.com/problems/maximum-sum-bst-in-binary-tree/

2 解题思路

1 采用后续遍历，(前中后遍历的前中后是针对root节点的访问时期和左右子树的比较)

2 对于每个节点，维持该节点的4个值：

int sum = 0; // 子树的所有和
int isBST = false; // 该节点为root的子树是否为BST
int maxVal = INT_MIN; // 该节点对应子树最大值

int minVal = INT_MAX; // 该节点对应子树最小值

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    struct entry {
        int sum = 0;
        int isBST = false;
        int maxVal = INT_MIN;
        int minVal = INT_MAX;
        entry() {};
    };
    map<void*, entry> bstRec;

    void dfs(TreeNode* root, int& res) {
        if(nullptr == root) {
            return;
        }
        dfs(root->left, res);
        dfs(root->right, res);

        // curRoot
        entry tmp;
        if(nullptr != root->left && nullptr != root->right) {
            tmp.sum = root->val + bstRec[root->right].sum + bstRec[root->left].sum;
            tmp.isBST = bstRec[root->right].isBST && \ 
                root->val < bstRec[root->right].minVal && \
                root->val > bstRec[root->left].maxVal;
            tmp.maxVal = max(root->val, bstRec[root->left].maxVal);
            tmp.maxVal = max(tmp.maxVal, bstRec[root->right].maxVal);
            tmp.minVal = min(root->val, bstRec[root->left].minVal);
            tmp.minVal = min(tmp.minVal, bstRec[root->right].minVal);
        } else if(nullptr == root->left && nullptr != root->right) {
            tmp.sum = root->val + bstRec[root->right].sum;
            tmp.isBST = bstRec[root->right].isBST && root->val < bstRec[root->right].minVal;
            tmp.maxVal = max(root->val, bstRec[root->right].maxVal);
            tmp.minVal = min(root->val, bstRec[root->right].minVal);
        } else if(nullptr != root->left && nullptr == root->right) {
            tmp.sum = root->val + bstRec[root->left].sum;
            tmp.isBST = bstRec[root->left].isBST && root->val > bstRec[root->left].maxVal;
            tmp.maxVal = max(root->val, bstRec[root->left].maxVal);
            tmp.minVal = min(root->val, bstRec[root->left].minVal);
        } else {
            tmp.sum = root->val;
            tmp.isBST = true;
            tmp.maxVal = root->val;
            tmp.minVal = root->val;
        } 
        if(tmp.isBST) {
            res = max(res, tmp.sum);
        } 
        // cout << root->val << " -> " << tmp.sum << endl;;
        bstRec[root] = tmp;

    }

    int maxSumBST(TreeNode* root) {
        int res = 0;
        dfs(root, res);
        return res;
    }
};

1569. 将子数组重新排序得到同一个二叉查找树的方案数

1 题目

https://leetcode-cn.com/problems/number-of-ways-to-reorder-array-to-get-same-bst/

2 解题思路

1 阅读提示即可，大致思路如下：
- 1.1 首先，意识到第一个数必然为二叉树的root，那么找出左边的节点和右边的节点分别记为lt，和rt
- 1.2 首先假设我们知道了以lt和rt的不改变子树结构的重排序方案数字为findWays(lt), findWays(rt)
- 1.3 那么我们只需要思考，如何利用1.2的结果来获得当前root的结果：
  - 很显然，我们只需要确定lt和rt在root对应的整个序列(长度记录为n)中放置方法有多少种方案？进一步分析：在不改变lt序列内部相对顺序的情况下，找出有多少繁殖lt序列的方法？那么不就是n-1中选出lt长度记为k个位置的方法数字吗？
  - 上述答案显而易见： c(n-1, k) = (n-1)!/(n-1-k)!/(k)!;
2 接着就是大数问题：由于n最大为1000，它的阶乘显然溢出，于是上面的直接计算阶乘的方案就失效，采用动动态规划的方法去算阶乘：
- c(n, k) = c(n-1, k) + c(n-1, k-1)
- 直观上来看假设原来只有n-1个物品选择k个，现在多加了一个物品，还是选择k个，那么方案数增加了：从 n 个物品中选择 k 个的方案数，等于从前 n-1 个物品中选择 k 个的方案数，加上从前 n-1 个物品中选择 k-1个（再选上第 nn 个物品）的方案数之和。

class Solution {
public:
    static constexpr long long largePrime = 1000000007;
    
    vector<long long> factorial;
    
    vector<vector<int>> c;

    int numOfWays(vector<int>& nums) {
        long long ans = 0;
        int n = nums.size();
        factorial.resize(1000, 1);
        // for(long long i = 1; i < 1000; ++i) {
        //     factorial[i] = i * (factorial[i-1] % largePrime);
        //     // cout << i << "->" << factorial[i] << endl;
        //     factorial[i] %= largePrime;
        // }
        
        c.assign(n, vector<int>(n));
        c[0][0] = 1;
        // cal c(n, m) = c(n-1, m) + c(n-1, m-1);
        for(int i = 1; i < n; ++i) {
            c[i][0] = 1;
            for(int j = 1; j < n; ++j) {
                c[i][j] = (c[i-1][j] + c[i-1][j-1]) % largePrime;
            }
        }
        
        ans = findWays(nums);

        return ans - 1;
    }

    long long findWays(vector<int>& nums) {
        int n = nums.size();
        if(n <= 2) {
            return 1;
        }
        
        int root = nums[0];
        vector<int> left;
        vector<int> right;
        for(int i = 1; i < nums.size(); ++i) {
            if(nums[i] < root) {
                left.emplace_back(nums[i]);
            } else {
                right.emplace_back(nums[i]);
            }
        }
        
        // that means:
        // for the left tree, all nodes shall seat in the other places(and not change the relative order)
        // except root pos find the way out(the way shall equal: 
        //     pick nodes size seat from all seats, that is c(n, m-1);
        // ) and mutiply the two subTree arrange way num
        int seats = n - 1;
        int nodesToSeat = left.size();
        // cout << "c(n, k) " << seats << " -> " << nodesToSeat << " = " << c[seats][nodesToSeat] << endl;
        // cout << "l r : " << findWays(left) << "  " << findWays(right) << endl;
        // return ((findWays(left)  % largePrime )* (findWays(right) % largePrime)) * (getWaysForCurLevel(seats, nodesToSeat) % largePrime);
        return findWays(left)  % largePrime * findWays(right) % largePrime * c[seats][nodesToSeat] % largePrime;
    }

    long long getWaysForCurLevel(int seats, int nodesToSeat) {
        cout << "c(n, k)2 :" << factorial[seats] << " " << factorial[nodesToSeat] << " " << factorial[seats - nodesToSeat] << endl;; 
        return factorial[seats] / factorial[nodesToSeat] / factorial[seats - nodesToSeat];
    }
};

0095. 不同的二叉搜索树 II

1 题目

https://leetcode-cn.com/problems/unique-binary-search-trees-ii/

2 解题思路

1 首先明确一点，递归的主体为，从nums的数组中返回对应的所有可能的bst树
- 1.1 输入： vector
- 1.2 返回： vector<treeNode*>
2 于是递归思路的想法就来了：
- 2.1 对于一个node如何生成其所有可能的二叉树呢？我们只考虑第1层到第2层的(因为其他所有层的递归都是一样的逻辑，除非返回层不太一样)
  - 2.1.1 从nums中选择一个作为root，左边的numsLeft和右边的numsRight分别获取root的所有左右子树
  - 2.1.2 递归调用函数从numsLeft得到leftTrees，相应的得到rightTrees
  - 2.1.3 得到leftTrees和rightTrees以后，采用2层for循环和root拼装，得到最后的树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<TreeNode*> generateTrees(int n) {
        vector<int> nodes;
        for(int i = 0; i < n; ++i) {
            nodes.emplace_back(i+1);
        }
        vector<TreeNode*> res;
        return getTreesFromArray(nodes);
    }

    vector<TreeNode*> getTreesFromArray(vector<int>& nodes) {
        int n = nodes.size();
        vector<TreeNode*> tmpRes;
        if(0 == n) {
            return {nullptr};
        }
        for(int i = 0; i < n; ++i) {
            int rootVal = nodes[i];
            vector<int> tmpLeft(nodes.begin(), nodes.begin() + i);
            vector<int> tmpRight(nodes.begin() + i + 1, nodes.end());
            vector<TreeNode*> left = getTreesFromArray(tmpLeft);
            vector<TreeNode*> right = getTreesFromArray(tmpRight);
            for(int m = 0; m < left.size(); ++m) {
                for(int n = 0; n < right.size(); ++n) {
                    TreeNode* root = new TreeNode(rootVal, left[m], right[n]); 
                    tmpRes.emplace_back(root); 
                }
            }
        }
        return tmpRes;
    }
}

0000 面试题 04.09. 二叉搜索树序列

1 题目

https://leetcode-cn.com/problems/bst-sequences-lcci/

2 解题思路

1 首先明确一点，递归的主体为，从root对应的tree中获取所有可能的bst子树序列
- 1.1 输入： treeNode*
- 1.2 返回： vector<vector>
2 于是递归思路的想法就来了：
- 2.1 对于一个root如何生成其所有可能的二叉树序列呢？我们只考虑第1层到第2层的(因为其他所有层的递归都是一样的逻辑，除非返回层不太一样)
  - 2.1.1 从root的左右子树获取其所有的左边子树序列lSeqs和右边子树序列rSeqs
  - 2.1.2 对lSeqs和rSeqs里的数据进行两两拼接，得到一组合合并序列，那么每一个两两拼接，可以获得很多个序列，具体拼接如下：
  - 2.1.3 那么很显然，记lSeqs和rSeqs中的一个两两拼接来自：lSeq，rSeq的长度分别为l和r，总长度为n，则有从n中选择l个的拼接方法，类似题目如下：
    1569. 将子数组重新排序得到同一个二叉查找树的方案数https://leetcode-cn.com/problems/number-of-ways-to-reorder-array-to-get-same-bst/

经典写法：

void selectKFromN(int st, int k, vector<vector<int>>& res, vector<int>& nums, vector<int>& tmpRes) {
    if(k == 0) {
        res.emplace_back(tmpRes);
        return;
    }
    for(int i = st; i < nums.size() - k + 1; ++i) {
        tmpRes.emplace_back(nums[i]);
        selectKFromN(i + 1, k - 1, res, nums, tmpRes);
        tmpRes.pop_back();
    }
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> BSTSequences(TreeNode* root) {
        return getSequencesFromRoot(root);
    }

    vector<vector<int>> getSequencesFromRoot(TreeNode* root) {
        if(nullptr == root) {
            return {{}};
        }
        
        vector<vector<int>> sequences;
        // for(auto seq : s) {
        //     s.emplace_back(root->val);
        // }
        // get left sequences and right
        vector<vector<int>> lSeqs = getSequencesFromRoot(root->left);
        vector<vector<int>> rSeqs = getSequencesFromRoot(root->right);
        int lSize = lSeqs[0].size();
        int rSize = rSeqs[0].size();
        
        // cout << "d0" << endl;
        // select lSize's positions in lSize + rSize + 1 's vector
        vector<vector<int>> res;
        vector<int> nums;
        for(int i = 0; i < lSize + rSize; ++i) {
            nums.emplace_back(i+1);
        }
        vector<int> tmpRes;
        // cout << "d1" << endl;
        selectKFromN(0, lSize, res, nums, tmpRes);
        
        int seqLen = lSeqs[0].size() + rSeqs[0].size() + 1;
        // cout << "d2 " << lSize << "@" << rSize << "=" << seqLen << endl;
            
        for(auto & lSeq : lSeqs) {
            for(auto & rSeq : rSeqs) {
                
                // cout << "d3" << endl;
                vector<int> tmpSeq(seqLen);
                tmpSeq[0] = root->val;

                for(auto & idxVecForLeft : res) {
                    int curLeft = 0;
                    int curRight = 0;
                    int lastLeft = 1;
                    vector<bool> forRight(seqLen, true);
                    
                    // cout << "d4" << endl;
                    for(auto lIdx : idxVecForLeft) {
                        tmpSeq[lIdx] = lSeq[curLeft++];
                        forRight[lIdx] = false;
                    }
                    for(int i = 1; i < seqLen; ++i) {
                        if(forRight[i]) {
                            tmpSeq[i] = rSeq[curRight++];
                        }
                    }
                    sequences.emplace_back(tmpSeq);
                }
            }
        }

        return sequences;
    }

    void selectKFromN(int st, int k, vector<vector<int>>& res, vector<int>& nums, vector<int>& tmpRes) {
        if(k == 0) {
            res.emplace_back(tmpRes);
            return;
        }
        for(int i = st; i < nums.size() - k + 1; ++i) {
            tmpRes.emplace_back(nums[i]);
            selectKFromN(i + 1, k - 1, res, nums, tmpRes);
            tmpRes.pop_back();
        }
    }
}

lcDisjointSetUnion1 - 并查集1

Posted on 2021-12-06 Edited on 2023-08-03

1 并查集

关键理解：并：是通过一条边将两个没有公共子集的集合合并，查：每个子集的所有子项对应的root是相同的

class DSU{
    public:
        vector<int> parent;
        vector<int> subTreeSize;
    
        DSU(int n) {
            parent.resize(n);
            subTreeSize.resize(n);
            for(int i = 0; i < n; ++i) {
                parent[i] = i;
                subTreeSize[i] = 1;
            }
        }
    
        int find(int x) {
            while(x != parent[x]) {
                parent[x] = parent[parent[x]];
                x = parent[x];
            }
            return x;
        }
    
        bool unionMerge(int x, int y) {
            int findX = find(x);
            int findY = find(y);
            if(findX != findY) {
                parent[findX] = findY;
                subTreeSize[findY] += subTreeSize[findX];
                return true;
            }
            return false;
        }

        int maxComponentSize() {
            return *max(subTreeSize.begin(), subTreeSize.end());
        }
    };

0952 最大因数联通分量大小

1 题目

https://leetcode-cn.com/problems/largest-component-size-by-common-factor

2 解题思路

个人体悟：当需要判断两个节点是否位于同一个连通子图时，首选并查集

1 普通思路：
- 1.1 很简单，暴力的去检测两两节点之间的连接性，然后构建并查集，求解最大的分量值即可；
2 优化思路：
- 1 中需要o(n^2)的复杂度去计算结点之间的链接性，我们不去计算节点的连接性，改为计算他们质数因子的连接性
- 2 对于每个数字提取出质因子列表，然后因为这个数的存在，可以将这些质因子联系起来，将所有数字的质因子计作L
- 3 而后我们统计每个数字，他对应的属于哪个质因子的联通分量，然后对该联通分量的root计数加1即可，最后找出所有的质因子联通分量最大的计数即可。

class Solution {
public:
    class DSU{
    public:
        vector<int> parent;
        vector<int> subTreeSize;
    
        DSU(int n) {
            parent.resize(n);
            subTreeSize.resize(n);
            for(int i = 0; i < n; ++i) {
                parent[i] = i;
                subTreeSize[i] = 1;
            }
        }
    
        int find(int x) {
            while(x != parent[x]) {
                parent[x] = parent[parent[x]];
                x = parent[x];
            }
            return x;
        }
    
        bool unionMerge(int x, int y) {
            int findX = find(x);
            int findY = find(y);
            if(findX != findY) {
                parent[findX] = findY;
                subTreeSize[findY] += subTreeSize[findX];
                return true;
            }
            return false;
        }

        int maxComponentSize() {
            return *max(subTreeSize.begin(), subTreeSize.end());
        }
    };

    int getGreatestCommonDivisor(int x, int y) {
        int res = 0;
        int mod = 0;
        do {
            mod = x % y;
            x = y;
            y = mod;

        } while(mod != 0);
        // cout << y << endl;
        return x;
    }

    int largestComponentSize(vector<int>& nums) {
        int n = nums.size();
        int maxComponentSize = INT_MIN;

        // DSU* dsu = new DSU(n);
        // travel all pairs and construct the dsu, o(n ** 2), too slow
        // for(int i = 0; i < n; ++i) {
        //     for(int j = i; j < n; ++j) {
        //         if(getGreatestCommonDivisor(nums[i], nums[j]) != 1) {
        //             dsu->unionMerge(i, j);
        //         }
        //     }
        // }
        // 
        // return *max_element(dsu->subTreeSize.begin(), dsu->subTreeSize.end());

        // we shall understand the fact that:
        // union: union by edeg, but edge denote two set

        // find a number's prime factors:
        map<int, vector<int>> numberToPrimes;
        for(auto num : nums) {
            vector<int> primes;
            int x = num;
            
            int d = 2;
            while(d * d <= num) {
                if(num % d == 0) {
                    // cull out all d
                    while(num % d == 0) {
                        num = num / d;
                    }
                    primes.emplace_back(d);
                }
                ++d;
            }
            if(num > 1 || primes.empty()) {
                primes.emplace_back(num);
            }
            numberToPrimes[x] = primes;
        }

        // form all the factors and numbers into nodes
        unordered_set<int> factors;
        for(auto& p : numberToPrimes) {
            for(auto& fac : p.second) {
                factors.insert(fac);
            }
        }

        unordered_map<int, int> facToNode;
        int i = 0;
        for(auto fac : factors) {
            facToNode[fac] = i++;
        }

        DSU* dsu = new DSU(factors.size());
        // union those numbers by factors
        for(auto p : numberToPrimes) {
            vector<int> primes = p.second;
            // union a number's all factors, we need union action: primes.size() times
            for(auto prime : primes) {
                // cout << p.first << "->" << prime << endl;
                dsu->unionMerge(facToNode[primes[0]], facToNode[prime]);
            }

        }

        // for each number, find the union root of this number
        // all numbers who are connected will share the same root
        vector<int> cnt(factors.size());
        for(auto p : numberToPrimes) {
            cnt[dsu->find(facToNode[p.second[0]])]++;
        }
        
        return *max_element(cnt.begin(), cnt.end());
        // return *max_element(dsu->subTreeSize.begin(), dsu->subTreeSize.end());
        // return dsu->maxComponentSize();
    }
};

0928 minMalwareSpread 最少病毒传播

1 题目

https://leetcode-cn.com/problems/minimize-malware-spread-ii/

2 解题思路

个人体悟：当需要判断两个节点是否位于同一个连通子图时，首选并查集

1 普通思路1
- 1.1 使用dfs，对于每个initial，则计算仅仅由他能传播到的节点有多少
2 使用并查集：
- 明确目标：对于每个initial，则计算仅仅由他能传播到的节点有多少
- 那么就首先构造不含initial的一个图G
- 遍历initial中的每个顶点，那么G中每个root都可以知道会被哪些initial所影响
- 于是每个initial的贡献为仅仅被自己所连接的root（也就是仅由自己才能传播过去）（换句话说，若G中的一个连通子图，会被好几个initial传播，那么只删除一个initial是没办法改变这个联通子图会被传播的下场）

class Solution {
public:
    int find(vector<int>& parent, int x) {
        while(x != parent[x]) {
            parent[x] = parent[parent[x]];
            x = parent[x];
        }
        return x;
    }

    bool unionMerge(vector<int>& parent, vector<int>& subTreeSize, int x, int y) {
        int findX = find(parent, x);
        int findY = find(parent, y);
        if(findX != findY) {
            parent[findX] = findY;
            subTreeSize[findY] += subTreeSize[findX];
            return true;
        }
        return false;
    }


    int minMalwareSpread(vector<vector<int>>& graph, vector<int>& initial) {
        // 对于每个initial计数的方式发生了改变，考虑一个不含有inital 的图，initial的得分应该是单独被他影响的子集
        int n = graph.size();
        vector<int> parent(n);
        for(int i = 0; i < n; ++i) {
            parent[i] = i;
        }
        
        vector<bool> isInitial(n, false);
        for(auto& i : initial) {
            isInitial[i] = true;
        }

        vector<int> subTreeSize(n, 1);
        // 构造union find set
        for(int i = 0; i < n; ++i) {
            if(isInitial[i]) {
                continue;
            }
            for(int j = 0; j < n; ++j) {
                if(1 == graph[i][j] && !isInitial[j]) {
                    unionMerge(parent, subTreeSize, i, j);
                }
            }
        }

        // for(int i = 0; i < n; ++i) {
        //     cout << "root " << i << " -> size " << subTreeSize[i] << endl;
        // }
        
        // find componets infected by a initial
        unordered_map<int, unordered_set<int>> initialToComponents;
        unordered_map<int, int> rootToInitial;
        for(auto& i : initial) {
            unordered_set<int> components;
            for(int v = 0; v < n; ++v) {
                if(!isInitial[v]) {
                    if(graph[i][v] == 1) {
                        int root = find(parent, v);
                        components.insert(root);
                        // cout << " ||| " << i << " >> " << root << endl;
                        // no occupied by single initial
                        if(rootToInitial.find(root) != rootToInitial.end() && \
                        rootToInitial[root] != i) {
                            rootToInitial[root] = -1;
                            continue;
                        }
                        rootToInitial[root] = i;
                    }
                }
            }
            initialToComponents[i] = components;
        }


        // cal scores for each initial
        int resInit = INT_MAX;
        int maxScore = INT_MIN;
        for(auto& p : initialToComponents) {
            int curInit = p.first;
            unordered_set<int> components = p.second;
            int score = 0;
            for(auto& root : components) {
                // std::cout << curInit << " -> " << score  << " with com: " << root << endl;
                if(rootToInitial[root] != -1) {
                    score += subTreeSize[root];
                    // cout << "added!" << endl;
                }
            }
            if(score > maxScore || (score == maxScore && curInit < resInit)) {
                maxScore = score;
                resInit = curInit;
            }
        }

        return resInit;
    }
};

0924 minMalwareSpread 最少病毒传播

1 题目

https://leetcode-cn.com/problems/minimize-malware-spread/

2 解题思路

个人体悟：当需要判断两个节点是否位于同一个连通子图时，首选并查集

1 普通思路1
- 1.1 考虑每个候选移除顶点，bfs看它能传播多少，如果传播的过程中遇到任何其他候选点，这说明减少该候选点和其位于同一个子图的候选点都是无法减少病毒传播的
- 1.2 之后我们得到那些候选移除顶点，他们各自的连通子图中就没有其他候选点，我们看连通子图大小，找出子图最大的那个候选点，作为结果输出。
- 1.3 若没有1.2中的候选点，则根本无法减少传播，于是直接输出所有候选点中的最小值即可。
2 使用并查集或者bfs来上色

同方法一一样，也得找出图中所有的连通分量，不同的是这一步用并查集来做。

在并查集中会额外计算连通分量的大小，当合并两个连通分量的时候，会把它们的大小进行累加。

借助并查集，可以用方法一中一样的思路处理：对于 initial 中每个颜色唯一的节点，都去计算连通分量的大小，从中找到最优解。如果 initial 中没有颜色唯一的节点，直接返回 min(initial)。

简洁起见，实现的并查集没有根据 rank 合并，这会让渐进复杂度变大一点。

class Solution {
public:
    int find(vector<int>& parent, int x) {
        while(x != parent[x]) {
            parent[x] = parent[parent[x]];
            x = parent[x];
        }
        return x;
    }

    bool unionMerge(vector<int>& parent, vector<int>& subTreeSize, int x, int y) {
        int findX = find(parent, x);
        int findY = find(parent, y);
        
        if(findX != findY) {
            parent[findX] = findY;
            subTreeSize[findY] += subTreeSize[findX];
            return true;
        }
        return false;
    }

    int minMalwareSpread(vector<vector<int>>& graph, vector<int>& initial) {
        int n = graph.size();
        vector<int> parent(n);
        vector<int> subTreeSize(n);

        for(int i = 0; i < n; ++i) {
            parent[i] = i;
            subTreeSize[i] = 1;
        }
        
        map<int, int> connectSizeToInitial; 
        // cal each connected component's size, attach initial with a component's "color"
        for(int i = 0; i < n; ++i) {
            for(int j = 0; j < n; ++j) {
                if(graph[i][j] == 1) {
                    unionMerge(parent, subTreeSize, i, j);
                }
            }
        }

        map<int, int> rootToInit;
        
        // if two initial number in same connected component, then remove one of them
        // will cause the same malware spread result
        // each color pick a smallest idx as res candidate in initial, finally pick the max connect size
        // find max connected size
        int maxConnectSize = INT_MIN;
        for(auto& i : initial) {
            int curRoot = find(parent, i);
            // cout << i << " ->> " << curRoot << endl;
            if(rootToInit.find(curRoot) != rootToInit.end()) {
                rootToInit[curRoot] = -1;
                continue; 
            }
            rootToInit[curRoot] = i;
        }

        bool hasLonelyInitial = false;
        for(auto& i : initial) {
            // those initial who do not share root
            if(rootToInit[find(parent, i)] != -1) { 
                // cout << "valid!" << endl;
                hasLonelyInitial = true;
                int curSubSize = subTreeSize[find(parent, i)];
                if(connectSizeToInitial.find(curSubSize) != connectSizeToInitial.end()) {
                    connectSizeToInitial[curSubSize] = min(connectSizeToInitial[curSubSize], i);
                    continue;
                }
                connectSizeToInitial[curSubSize] = i;
                maxConnectSize = max(maxConnectSize, curSubSize);
                // cout << maxConnectSize << endl;
            }
        }
        

        // for(auto& p : connectSizeToInitial) {
        //     cout << p.first << " -<<> " << p.second << endl;
        // }

        // for(auto& p : rootToInit) {
        //     cout << p.first << " -> " << p.second << endl;
        // }

        if(hasLonelyInitial) {
            return connectSizeToInitial[maxConnectSize];
        }
        return *min_element(initial.begin(), initial.end());
    }
}

0778 泳池游泳上升泳池

1 题目

https://leetcode-cn.com/problems/swim-in-rising-water/

2 解题思路

1 普通思路1
- 对于每一个水位，采用bfs算法看是否能够到达，那么对于水位可以用二分法加速o(logn),bfs要o(n^2)，所以o(n^2logn)
2 普通思路2
- 仔细理解改题目，问的是a和b什么时候能够连通的问题？那么自然就想到并查集，反复说一句哈：并查集并的子树，查的是子树的root
- 对于水位从低到高遍历，每次更新和当前水位相同高度的格子(注意，题目说的非常清除，所有的格子的值在0到n^2，且不同)和周围联通情况
- 每次更新完连通情况我们看一下是否能够使得左上角和右下角的两个节点相互连通即可。

class Solution {
public:
    int find(vector<int>& parent, int x) {
        while(x != parent[x]) {
            parent[x] = parent[parent[x]];
            x = parent[x];
        }

        return x;
    }

    bool unionMerge(vector<int>& parent, int x, int y) {
        int findX = find(parent, x);
        int findY = find(parent, y);
        if(findX != findY) {
            parent[findX] = findY
            return true;
        }
        return false;
    }

    int swimInWater(vector<vector<int>>& grid) {
        // for each threshold, maintain a unionFind
        // everytime increase thres, we modify the connection of unionFind
        int n = grid.size();

        if(n == 1) {
            return 0;
        }

        vector<int> parent(n * n);
        for(int i = 0; i < n * n; ++i) {
            parent[i] = i;
        }

        // Each value grid[i][j] is unique.
        vector<vector<int>> elevationToIdx(n * n, vector<int>(n));
        for(int i = 0; i < n; ++i) {
            for(int j = 0; j < n; ++j) {
                elevationToIdx[grid[i][j]][0] = i;
                elevationToIdx[grid[i][j]][1] = j;
            }
        }

        vector<vector<int>> moves = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
        for(int thres = 0; thres < n * n; ++thres) {
            // when the rain rise, process the exact the same height grid
            int tarX = elevationToIdx[thres][0];
            int tarY = elevationToIdx[thres][1];
            for(auto deltaXY : moves) {
                int newX = tarX + deltaXY[0];
                int newY = tarY + deltaXY[1];
                if(newX >= 0 && newY >= 0 && newX < n && newY < n && grid[newX][newY] <= thres) {
                    // cout << newX << " " << newY << "  ->" << thres <<endl;
                    unionMerge(parent, grid[newX][newY], grid[tarX][tarY]);
                    if(find(parent, grid[0][0]) == find(parent, grid[n - 1][n - 1])) {
                        return thres;
                    }
                }
            }
        }
        return n*n;
    }
}

shortestPath

Posted on 2021-11-30 Edited on 2023-08-03

1 dijstra算法

自wiki:

对于没有任何优化的戴克斯特拉算法，实际上等价于每次遍历了整个图的所有结点来找到Q(为图的点集)中满足条件的元素（即寻找最小的頂點是${\displaystyle O(|V|)}$的，此外实际上还需要遍历所有的边一遍，因此算法的复杂度是${\displaystyle O(|V|^{2}+|E|)}$
一个基于堆优化的实现：https://www.geeksforgeeks.org/dijkstras-shortest-path-algorithm-using-priority_queue-stl/

#include<bits/stdc++.h> 
using namespace std; 
# define INF 0x3f3f3f3f 
  
// iPair ==> Integer Pair（整数对）
typedef pair<int, int> iPair; 
  
// 加边
void addEdge(vector <pair<int, int> > adj[], int u, 
                                     int v, int wt) 
{ 
    adj[u].push_back(make_pair(v, wt)); 
    adj[v].push_back(make_pair(u, wt)); 
} 
   
  
// 计算最短路
void shortestPath(vector<pair<int,int> > adj[], int V, int src) 
{ 
    // 关于stl中的优先队列如何实现，参考下方网址：
    // http://geeksquiz.com/implement-min-heap-using-stl/ 
    priority_queue< iPair, vector <iPair> , greater<iPair> > pq; 
  
    // 距离置为正无穷大
    vector<int> dist(V, INF); 
    vector<bool> visited(V, false);

    // 插入源点，距离为0
    pq.push(make_pair(0, src)); 
    dist[src] = 0; 
  
    /* 循环直到优先队列为空 */
    while (!pq.empty()) 
    { 
        // 每次从优先队列中取出顶点事实上是这一轮最短路径权值确定的点
        int u = pq.top().second; 
        pq.pop(); 
        if (visited[u]) {
            continue;
        }
        visited[u] = true;
        // 遍历所有边
        for (auto x : adj[u]) 
        { 
            // 得到顶点边号以及边权
            int v = x.first; 
            int weight = x.second; 
  
            //可以松弛
            if (dist[v] > dist[u] + weight) 
            { 
                // 松弛 
                dist[v] = dist[u] + weight; 
                pq.push(make_pair(dist[v], v)); 
            } 
        } 
    } 
  
    // 打印最短路
    printf("Vertex Distance from Source\n"); 
    for (int i = 0; i < V; ++i) 
        printf("%d \t\t %d\n", i, dist[i]); 
} 
int main() 
{ 
    int V = 9; 
    vector<iPair > adj[V]; 
    addEdge(adj, 0, 1, 4); 
    addEdge(adj, 0, 7, 8); 
    addEdge(adj, 1, 2, 8); 
    addEdge(adj, 1, 7, 11); 
    addEdge(adj, 2, 3, 7); 
    addEdge(adj, 2, 8, 2); 
    addEdge(adj, 2, 5, 4); 
    addEdge(adj, 3, 4, 9); 
    addEdge(adj, 3, 5, 14); 
    addEdge(adj, 4, 5, 10); 
    addEdge(adj, 5, 6, 2); 
    addEdge(adj, 6, 7, 1); 
    addEdge(adj, 6, 8, 6); 
    addEdge(adj, 7, 8, 7); 
  
    shortestPath(adj, V, 0); 
  
    return 0; 
}

2 Floyd算法

空间o(n^2)，时间o(n^3):
自wiki

1 let dist be a |V| × |V| array of minimum distances initialized to ∞ (infinity)
2 for each vertex v
3    dist[v][v] ← 0
4 for each edge (u,v)
5    dist[u][v] ← w(u,v)  // the weight of the edge (u,v)
6 for k from 1 to |V|
7    for i from 1 to |V|
8       for j from 1 to |V|
9          if dist[i][j] > dist[i][k] + dist[k][j] 
10             dist[i][j] ← dist[i][k] + dist[k][j]
11     end if

lcGraphUndirected1 - 无向图题集1

Posted on 2021-11-29 Edited on 2023-08-03

0 一些基础

判断整个图是否连通

使用dfs判断整个图是否连通：

// if not connected, return false
vecctor<int> stack = {0};
vector<bool> vis(graph.size(), false);
vis[0] = true;
int visCnt = 1;
// dfs to check if connected
while(!stack.empty()) {
    int top = stack.back();
    bool allVisited = true;
    for(int i = 0; i < graph[top].size(); ++i) {
        if(!vis[graph[top][i]]) {
            stack.emplace_back(graph[top][i]);
            vis[graph[top][i]] = true;
            allVisited = false;
            visCnt++;
            break;
        }
    }
    if(allVisited) {
        stack.pop_back();
    }
}

if(visCnt != n) return false;

使用bfs也是可以的，比如下面的0684-冗余链接

并查集的使用

主要是将有关联的边聚合到同一个root里去，可以压缩路径加速find过程

int find(vector<int>& parent, int curNode) {
    while(parent[curNode] != curNode) {
        parent[curNode] = parent[parent[curNode]];
        curNode = parent[curNode];
    }
    return curNode;
}

void unionMerge(vector<int>& parent, int from, int to) {
    int x = find(parent, from);
    int y = find(parent, to);
    
    if(x != y) {
        parent[x] = y;
    }
}

二分图判断

1 普通思路
使用bfs遍历，考虑奇偶层级，奇层级为节点集合A，偶层级为节点集合B，最后扫描一遍所有的边，判断是否有边位于AB而不是横跨AB的，
有的话返回false，不然则true
2 并查集
3 dfs

实例讲解

0785 是否二分图

1 题目

https://leetcode-cn.com/problems/is-graph-bipartite/

2 解题思路

1 普通思路
使用bfs遍历，考虑奇偶层级，奇层级为节点集合A，偶层级为节点集合B，最后扫描一遍所有的边，判断是否有边位于AB而不是横跨AB的，
有的话返回false，不然则true；
同时注意邻接表的判空，所有边个数为0为空的图，是可以二分的哦！

class Solution {
public:
    bool isBipartite(vector<vector<int>>& graph) {
        int n = graph.size();
        
        int edgeNum = 0;
        for(int u = 0; u < n; ++u) {
            for(int v = 0; v < graph[u].size(); ++v) {
                ++edgeNum;
            }
        }
        if(edgeNum == 0) return true;

        // if not connected, return false
        vector<int> stack = {0};
        // vector<bool> vis(graph.size(), false);
        // vis[0] = true;
        // int visCnt = 1;
        // // dfs to check if connected
        // while(!stack.empty()) {
        //     int top = stack.back();
        //     bool allVisited = true;
        //     for(int i = 0; i < graph[top].size(); ++i) {
        //         if(!vis[graph[top][i]]) {
        //             stack.emplace_back(graph[top][i]);
        //             vis[graph[top][i]] = true;
        //             allVisited = false;
        //             visCnt++;
        //             break;
        //         }
        //     }
        //     if(allVisited) {
        //         stack.pop_back();
        //     }
        // }

        // if(visCnt != n) return false;

        // bfs to judge biPartitable
        deque<int> q = {};


        vector<bool> vis2(graph.size(), false);
            unordered_set<int> biPart1 = {};
            unordered_set<int> biPart2;
            deque<int> level = {};
        int bfsNum = 0;
        
        while(bfsNum != n) {        

            for(int i = 0; i < n; ++i) {
                if(!vis2[i]) {
                    q.emplace_back(i);
                    level.emplace_back(0);
                    biPart1.insert(i);
                    ++bfsNum;
                    vis2[i] = true;
                    break;
                }
            }
            while(!q.empty()) {
                int front = q.front();
                for(int i = 0; i < graph[front].size(); ++i) {
                    if(!vis2[graph[front][i]]) {
                        q.emplace_back(graph[front][i]);
                        ++bfsNum;
                        level.emplace_back(level.front() + 1);
                        if(level.front() % 2 == 0) {
                            biPart2.insert(graph[front][i]);
                        } else {
                            biPart1.insert(graph[front][i]);
                        }
                        vis2[graph[front][i]] = true;          
                    }
                }
                q.pop_front();
                level.pop_front();
            }
            // for(auto& i : biPart1) {
            //     std::cout << i << " ";
            // }
            // cout << endl;
            // for(auto& i : biPart2) {
            //     std::cout << i << " ";
            // }
            // cout << endl;
            
            for(int u = 0; u < n; ++u) {
                for(int v = 0; v < graph[u].size(); ++v) {
                    if((biPart2.count(u) == 1 && biPart2.count(graph[u][v]) == 1) || \
                    (biPart1.count(u) == 1 && biPart1.count(graph[u][v]) == 1)) {
                        return false;
                    }
                }
            }
        }


        return true;
    }
}

0765minSwapsCouple

1 题目

https://leetcode-cn.com/problems/couples-holding-hands/

2 解题思路

0 一句话：找连通子图，每个连通子图节点数－1之和即为结果
1 普通思路
对于每一个2k - 2， 2k - 1的连续两个座位去找，2k - 2上的人的情侣，把它换到2k - 1位置上，遍历k即可 o(n**2)

2 改进思路
考虑到这样一个事实：
如果有8个座位，然后所有情侣都没办法相邻而坐，则考虑：将在2k-2和2k-1座位上的相邻两人但不是情侣创建一条边，节点则是情侣的cp序号
(比如4,5序号的情侣对应一个节点，为5/2 == 4/2 == 2)
然后我们可以知道，这个图只有一个连通子图，然后其节点数量为4，那么需要交换的次数为4-1 = 3，

容易被迷惑的地方：一次交换至少能够完成一对情侣，只有最后的一次交换能够完成两队情侣，其余均只能完成一次
所以说这个最小交换次数，其实别反复换，算出来的就是最小的

class Solution {
public:
    int minSwapsCouples(vector<int>& row) {
        // 容易被迷惑的地方： 一次交换至少能够完成一对情侣，只有最后的一次交换能够完成两队情侣，其余均只能完成一次
        // 所以说这个最小交换次数，其实别反复换，算出来的就是最小的
        
        // 首先注意到，将2个情侣看成一个节点，如果不属于一对的情侣坐在2k - 2, 2k - 1的两个位置上，则连一条线
        vector<int> parent(row.size() / 2);
        for(int i = 0; i < row.size() / 2; ++i) {
            parent[i] = i;
        }

        for(int i = 0; i < row.size(); i += 2) {
            int nodeIdx = i / 2;
            unionMerge(parent, row[i] / 2, row[i + 1] / 2);
            // std::cout << row[i] / 2<< " -> " << row[i + 1] / 2 << std::endl;
        }

        // 找出上图所有连通子图, 所有连通子图的边的节点个数减去1得到一个子图所有情侣相邻而坐需要的交换次数
        unordered_map<int, int> rootIdxToCnt;
        for(int i = 0; i < row.size() / 2; ++i) {
            rootIdxToCnt[find(parent, i)] ++;
            // std::cout << i << " -> " << find(parent, i) << std::endl;
        }

        int res = 0;
        for(auto& it : rootIdxToCnt) {
            res += it.second - 1;
        }
        return res;

    }

    int find(vector<int>& parent, int curNode) {
        while(parent[curNode] != curNode) {
            parent[curNode] = parent[parent[curNode]];
            curNode = parent[curNode];
        }
        return curNode;
    }

    void unionMerge(vector<int>& parent, int from, int to) {
        int x = find(parent, from);
        int y = find(parent, to);
        
        if(x != y) {
            parent[x] = y;
        }
    }
}

0684 冗余链接

1 题目描述

https://leetcode-cn.com/problems/redundant-connection

2 解题思路

使用并查集，将每一条边都看做一个子树，然后一条边一条边加入这个树，当加入的边的两个顶点属于同一个子树时，就认为有回环，则返回这个冗余边。
见如下代码：

class Solution {
public:
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        tree.resize(edges.size() * 2 + 1, -1);
        subTreeSize.resize(edges.size() * 2 + 1, 1);
        
        vector<int> res;
        for(auto& c : edges) {
            if(!unionMerge(c[0], c[1], tree)) {
                res = c;
                break;
            }
        }
        return res;
    }
    
    int find(int tar, vector<int>& tree) {
        int curFather = tree[tar];
        if (curFather < 0) { // tar has no father, so he is the root
            tree[tar] = tar;
            return tar;
        }
        if(tar != curFather) {
            tree[tar] = find(curFather, tree); // compress the data path
        }
        return tree[tar];
    }
    
    
    bool unionMerge(int x, int y, vector<int>& tree) {
        int fx = find(x, tree);
        int fy = find(y, tree);
        if(fx == fy) {
            return false; // x, y are in the same tree, need no merge
        }
        if(subTreeSize[fx] >= subTreeSize[fy]){ // merge by rank of the sub Tree
            tree[fy] = fx;
            subTreeSize[fx] += subTreeSize[fy];
        } else {
            tree[fx] = fy;
            subTreeSize[fy] += subTreeSize[fx];
        }
        return true;
    }
    
    vector<int> subTreeSize;
    vector<int> tree;
};

lcDictOrderAndPermutation - 字典序和全排列

Posted on 2021-11-26 Edited on 2023-08-03

0 全排列算法

0.1 全排列实现

1 一个排列，其优先交换靠右的位置的数字来获得下一个排列，比如1 2 3，他下一个必定是交换2 3,1不会参与其中，
2 意识到一个排列，左侧属于高位，打个比方，若全排列对应的都有一个数字表示该排列的大小，那么左侧值越大，那么排列越大

# ref: https://blog.51cto.com/u_4925054/884291
全排列（非递归求顺序）算法  
1、建立位置数组，即对位置进行排列，排列成功后转换为元素的排列；  
2、按如下算法求全排列：  
    设P是1～n(位置编号)的一个全排列：p = p1,p2...pn = p1,p2...pj-1,pj,pj+1...pk-1,pk,pk+1...pn  
    (1)从排列的尾部开始，找出第一个比右边位置编号小的索引j（j从首部开始计算），即j = max{i | pi < pi+1}  
    (2)在pj的右边的位置编号中，找出最后一个比pj大的位置编号索引k，即 k = max{i | pi > pj} (k > j)
    (3)交换pj与pk  
    (4)再将pj+1...pk-1,pk,pk+1...pn翻转得到排列p' = p1,p2...pj-1,pj,pn...pk+1,pk,pk-1...pj+1  
    (5)p'便是排列p的下一个排列  

例如：  
24310是位置编号0～4的一个排列，求它下一个排列的步骤如下：  
(1)从右至左找出排列中第一个比右边数字小的数字2；  
(2)在该数字后的数字中找出比2大的数中编号最大的3；  
(3)将2与3交换得到34210；  
(4)将原来2（当前3）后面的所有数字翻转，即翻转4210，得30124；  
(5)求得24310的下一个排列为30124。

这里给出官方的可能实现：
5 6 1 2 3 4的下一个排列是： 6 1 2 3 4 5

0.2 迭代实现

// 比如求 6 5 4 2 3 1的下一个排列
template<class BidirIt>
bool next_permutation(BidirIt first, BidirIt last)
{
    if (first == last) return false;
    BidirIt i = last;
    if (first == --i) return false;
 
    while (true) {
        BidirIt i1, i2;
 
        i1 = i;
        if (*--i < *i1) { // i = prev(i1), 找到了一个 i < i1的(2 < 3)相邻对子
            i2 = last;
            while (!(*i < *--i2)) // 从i的右边找最后一个比i大的数字
                ;
            std::iter_swap(i, i2); // 交换 i和i2 (2,3),变成6 5 4 3 2 1
            std::reverse(i1, last); // 从i1(原始数据中的3处)到最后，得到 6 5 4 3 1 2
            return true;
        }
        if (i == first) { // 若果找不到两个相邻的数，使得右边<左边,则认为是最大排列
            std::reverse(first, last);
            return false;
        }
    }
}

2 回溯

void chooseN3(vector<char>& dq, int n, priority_queue<string, vector<string>, std::function<bool(string, string)>>& res, string& tmpRes) {
    if(n == 0) {
        res.push(tmpRes);
        // std::cout << "-d2 " << tmpRes << " with n = " << tmpRes.size() <<std::endl;
        return;
    }
    for(int i = 0; i < dq.size(); ++i) {
        tmpRes.push_back(dq[i]);
        vector<char> tmpDq;
        tmpDq.insert(tmpDq.end(), dq.begin(), dq.begin() + i);
        tmpDq.insert(tmpDq.end(), dq.begin() + i + 1, dq.end());
        chooseN3(tmpDq, n - 1, res, tmpRes);
        tmpRes.pop_back();
    }
}

2014 重复 K 次的最长子序列

1 题目

https://leetcode-cn.com/problems/largest-color-value-in-a-directed-graph/

2 解题思路

1 自己的思路：首先查出来哪些字符有k个，压入dq中，若一个字符有2k个，则压入两次(代表最终结果里可以有两个该字符)，而后将其逆序排序
2 那么最后的结果一定是从dq中来，我们可以枚举dq的所有子序列即可(枚举子序列需要按照逆序字典序，这样找到的第一个子序列即为我们的目标)

关键: 如何获得逆序子序列呢？

1.1 最简单的想法，从dq(已经是最大的子序列了)中选择长度为n(7到1)的子序列，获取每个子序列(由于父序列为最大序列，那么子序列也一定是最大序列)所有的全排列
1.2 但是这样做有问题，比如有fd，fe两个子序列，那么优先对于fe去看其所有的排列是否满足要求，然而若是ef满足要求，那么其检测顺序在fd前面，

这样就没有满足按照逆序字典序的方法去检测，于是对于长度为n的子序列，需要先生成所有的全排列，然后按照字典序排序，
最后中实现总代码：

class Solution {
public:
    string longestSubsequenceRepeatedK(string s, int k) {
        // 找出大于等于k的字符记作kSet
        int n = s.size();

        vector<int> cnt(26, 0);
        vector<char> dq;
        for(int i = 0; i < n; ++i) {
            int charNo = s[i]-'a';
            ++cnt[charNo];
            if(cnt[charNo] % k == 0) {
                dq.push_back(s[i]);
            }
        }

        // 将kSet按照逆序字典序排序
        auto cmp = [](char a, char b) {return a > b;};
        sort(dq.begin(), dq.end(), cmp);

            // string tmp = "";
            // for(char& c : dq) tmp += c;
            // std::cout << "-d1 " << tmp << std::endl;


        // 找到第一个满足的最大长度为dq的字典序逆序的子序列的排列即为结果
        // 从子模式串的最大长度dq.size()一直遍历到1
        for(int len = dq.size(); len >= 1; --len) {
            // vector<char> tmp;
            // vector<vector<char>> res;
            // chooseN(dq, len, 0, res, tmp);
            // string tmp;
            // vector<string> res;
            // chooseN2(dq, len, 0, res, tmp);

            // // 构建出同len的所有permutaion，然后sort然后再来以此比较
            // vector<string> sameLenStr;
            // for(int i = 0; i < res.size(); ++i) {
            //     do {

            //         // string tmp4 = "";
            //         // for(char& c : res[i]) tmp4 += c;
            //         // std::cout << "-d4 " << tmp4 << " with n = " << len <<std::endl;
            //         sameLenStr.push_back(res[i]);
            //     }while(prev_permutation(res[i].begin(), res[i].end()));
            // }
            // sort(sameLenStr.begin(), sameLenStr.end(), [](string a, string b){return a > b;});
                        // for(int subIdx = 0; subIdx < sameLenStr.size(); ++subIdx) {
            //     // do {
            //     // 构造seq*k
            //     string tmpDq;
            //     for(int i = 0; i < k; ++i) {
            //         tmpDq += sameLenStr[subIdx];
            //     }
// 
            //     // string tmp3 = "";
            //     // for(char& c : tmpDq) tmp3 += c;
            //     // std::cout << "-d3 " << tmp3 << " with n = " << tmpDq.size() <<std::endl;
// 
            //     // 判断构造的seq*k是否存在于s中
            //     int tmpIdx = 0;
            //     int realIdx = 0;
            //     int cnt = 0;
            //     for(; tmpIdx < tmpDq.size(); ++tmpIdx) {
            //         for(; realIdx < n; ++realIdx) {
            //             if(s[realIdx] == tmpDq[tmpIdx]) {
            //                 ++cnt;
            //                 ++realIdx;
            //                 break;
            //             }
            //         }
            //     }
// 
            //     
            //     if(cnt == tmpDq.size()) {
            //         return sameLenStr[subIdx];
            //     }
            //         
            // }
            string tmp;
            std::function<bool(string, string)> cmp = [](string a, string b)->bool{return a < b;};
            priority_queue<string, vector<string>, std::function<bool(string, string)>> sameLenStr(cmp);
            chooseN3(dq, len, sameLenStr, tmp);
 
            // 看该子序列是否可以
            while(!sameLenStr.empty()) {
                string curStr = sameLenStr.top();
                sameLenStr.pop();
                string tmpDq;
                for(int i = 0; i < k; ++i) {
                    tmpDq += curStr;
                }

                // string tmp3 = "";
                // for(char& c : tmpDq) tmp3 += c;
                // if(curStr.size() <= 10)std::cout << "-d3 " << curStr << " with n = " << tmpDq.size() <<std::endl;

                // 判断构造的seq*k是否存在于s中
                int tmpIdx = 0;
                int realIdx = 0;
                int cnt = 0;
                for(; tmpIdx < tmpDq.size(); ++tmpIdx) {
                    for(; realIdx < n; ++realIdx) {
                        if(s[realIdx] == tmpDq[tmpIdx]) {
                            ++cnt;
                            ++realIdx;
                            break;
                        }
                    }
                }

                if(cnt == tmpDq.size()) {
                    return curStr;
                }
            }

        }
        return "";
    }

    void chooseN2(vector<char>& dq, int n, int st, vector<string>& res, string& tmpRes) {
        if(n == 0) {
            res.push_back(tmpRes);
            // std::cout << "-d2 " << tmpRes << " with n = " << tmpRes.size() <<std::endl;
            return;
        }
        for(int i = st; i < dq.size() - n + 1; ++i) {
            tmpRes.push_back(dq[i]);
            chooseN2(dq, n - 1, i + 1, res, tmpRes);
            tmpRes.pop_back();
        }
    }

    void chooseN3(vector<char>& dq, int n, priority_queue<string, vector<string>, std::function<bool(string, string)>>& res, string& tmpRes) {
        if(n == 0) {
            res.push(tmpRes);
            // std::cout << "-d2 " << tmpRes << " with n = " << tmpRes.size() <<std::endl;
            return;
        }
        for(int i = 0; i < dq.size(); ++i) {
            tmpRes.push_back(dq[i]);
            vector<char> tmpDq;
            tmpDq.insert(tmpDq.end(), dq.begin(), dq.begin() + i);
            tmpDq.insert(tmpDq.end(), dq.begin() + i + 1, dq.end());
            chooseN3(tmpDq, n - 1, res, tmpRes);
            tmpRes.pop_back();
        }
    }
  
};

0047 全排列去重

1 题目

https://leetcode-cn.com/problems/permutations-ii/

2 解题思路

class Solution {
public:
    unordered_set<string> hash;

    vector<vector<int>> permuteUnique(vector<int>& nums) {
        // vector<vector<int>> res;
        // vector<int> tmp;
        // string tmpStr = "";
        // chooseN(nums, nums.size(), res, tmp, tmpStr);
        // vector<vector<int>> res;
        // vector<int> tmp;
        // string tmpStr = "";
        // chooseN2(nums, 0, nums.size(), res, tmpStr);
        vector<vector<int>> res;
        vector<int> tmp;
        vector<bool> vis(nums.size(), false);
        sort(nums.begin(), nums.end());
        chooseN3(nums, 0, nums.size(), res, vis, tmp);
        return res;
    }

    // 160ms
    void chooseN(vector<int>& nums, int n, vector<vector<int>>& res, vector<int>& tmp, string tmpStr) {
        if(n == 0) {
            if(hash.count(tmpStr) == 0) {
                std::cout << tmpStr << std::endl;
                hash.insert(tmpStr);
                res.emplace_back(tmp);
            }
        }

        for(int i = 0; i < nums.size(); ++i) {
            
            vector<int> tmpNums;
            tmpNums.insert(tmpNums.end(), nums.begin(), nums.begin() + i);
            tmpNums.insert(tmpNums.end(), nums.begin() + i + 1, nums.end());
            tmp.emplace_back(nums[i]);
            tmpStr.push_back(static_cast<char>(nums[i] + 107));
            chooseN(tmpNums, n-1, res, tmp, tmpStr);
            tmpStr.pop_back();
            tmp.pop_back();
        }
    }


   
    // chooseN由于每次构造新的串子，这样降低了速度，只用swap到最左边就行了
    // 32ms
    void chooseN2(vector<int>& nums, int st, int n, vector<vector<int>>& res, string tmpStr) {
        if(st == nums.size()) {
            if(hash.count(tmpStr) == 0) {
                std::cout << tmpStr << std::endl;
                hash.insert(tmpStr);
                res.emplace_back(nums);
            }
        }

        for(int i = st; i < nums.size(); ++i) {
            
            vector<int> tmpNums;
            tmpStr.push_back(static_cast<char>(nums[i] + 107));
            swap(nums[st], nums[i]);
                      
            chooseN2(nums, st + 1, nums.size(),  res, tmpStr);

            swap(nums[st], nums[i]);
            tmpStr.pop_back();
        }
    }

    // 由于使用string来判断还是降低了速度，于是在搜索过程中判断是否能够压入
    void chooseN3(vector<int>& nums, int st, int n, vector<vector<int>>& res, vector<bool>& vis, vector<int>& tmp) {
        if(st == nums.size()) {
                res.emplace_back(tmp);
        }

        for(int i = 0; i < nums.size(); ++i) {
            // 如果当前数作为第st层的回溯已经用过了，则不再使用 || 若当前数字和st层上一次使用数字相同，则也不再使用
            if(vis[i] || (i > 0 && nums[i] == nums[i - 1] && !vis[i - 1])) {
                continue;
            }
            // if (vis[i] || (i > 0 && nums[i] == nums[i - 1] && !vis[i - 1])) {
            //     continue;
            // }
            vector<int> tmpNums;
            tmp.emplace_back(nums[i]);
            vis[i] = 1;
                      
            chooseN3(nums, st + 1, nums.size(),  res, vis, tmp);

            vis[i] = 0;
            tmp.pop_back();
            // swap(nums[st], nums[i]);
        }
    }
};

lcGraphDirected1 - 有向图 1

Posted on 2021-11-24 Edited on 2023-08-03

0 有向图的环路判断

1 bfs访问节点的数目超过n本身才能说明有环
2 或者dfs能够访问到之前访问过的节点，也说明有环
3 不能仅仅通过是否有出度为0的节点来判断是否成环，eg:
[[0,1],[1,1]]

1857largestPathValue 路径最大节点颜色数

1 题目

https://leetcode-cn.com/problems/largest-color-value-in-a-directed-graph/

2 解题思路

1 自己的思路：自然能够想到的解题方法, 对于出度为0的点做dfs，然后统计每个颜色的值
2 思路存在的问题：

上述算法的遍历节点总是从出度为0的地方开始遍历所有可能的路径
有重复计算的第方，想象一下，1, 2分别连着3,3后面跟了1000个节点
那么会从1,2分别计算一遍，那3后面的1000个节点被重复计算了2次

3 解决思路：

很显然我们就会想到从小规模开始计算，那么1,2的计算结果就能利用
小规模的值得到了,那么什么样的节点算是小规模子图的起始点？
这隐藏了一个拓扑排序 + 动态规划的思路在其中：
如果想要减少上述重复计算过程，可以考虑使用动态规划，但是
需要直到1,2,3以及后面节点谁在前谁在后的问题，使用拓扑排序解决
这里可以顺便说一下
首先bfs获得拓扑排序，依此入栈s，(则s的栈顶得到的是没有后继节点的
那些节点)，则依此从s中pop然后得到节点v，dp[v][c]代表从v出发的
颜色为c的最大值，则对于每个有到达v的边的u，有：
dp[u][c] = max(dp[u][c], dp[v][c]);
但是这个需要知道，v的前级节点有哪些，则需要翻转一遍v，所以就
bfs拓扑排序依此入队列，从队头出数据(这些数据都是没有入度的)，
dp[v][c] 表示到达节点v的所有路径的颜色为c的最大值(并未统计v节点本身)
对于u所有的 -> v:
dp[v][c] = max(dp[u][c], dp[v][c]); // 广度优先遍历

class Solution {
public:
    int ans = -1;

    void dfs(int from, string& colors, vector<vector<int>>& g, map<char, int>& cntInPath) {
        cntInPath[colors[from]]++;
        ans = max(ans, cntInPath[colors[from]]);
        for(int to = 0; to < g.size(); ++to) {
            if(g[from][to] == 1) {
                dfs(to, colors, g, cntInPath);
            }
        }
        cntInPath[colors[from]]--;
    }

    int largestPathValue(string colors, vector<vector<int>>& edges) {
        // // 自然能够想到的解题方法: 
        // // 基于出度为0的点做dfs，然后统计每个颜色的值
        // vector<int> noInNode;
        // map<int, int> inDegreeStatistic;
        // for(auto &e : edges) {
        //     inDegreeStatistic[e[1]]++;
        // }
        // int n = colors.size();
        // for(int i = 0; i < n; ++i) {
        //     auto it = inDegreeStatistic.find(i);
        //     if(it == inDegreeStatistic.end()) {
        //         noInNode.emplace_back(i);
        //     }
        // }

        // if(noInNode.size() == 0){
        //     return -1;
        // }

        // vector<vector<int>> g(n, vector<int>(n, -1));
        // for(int i = 0; i < edges.size(); ++i) {
        //     g[edges[i][0]][edges[i][1]] = 1;
        // }

        // // 对每一个节点出度为0的遍历
        // int maxApperanceNumInPath = -1;
        // map<char, int> cntInPath;
        // for(auto& c : colors) {
        //     cntInPath[c] = 0;
        // }
        // for(auto& n : noInNode) {
        //     dfs(n, colors, g, cntInPath);
        // }

        // 上述算法的遍历节点总是从出度为0的地方开始遍历所有可能的路径
        // 有重复计算的第方，想象一下，1, 2分别连着3,3后面跟了1000个节点
        // 那么会动1,2分别计算一遍，那3后面的1000个节点被重复计算了2次
        // 很显然我们就会想到从小规模开始计算，那么1,2的计算结果就能利用
        // 小规模的值得到了,那么什么样的节点算是小规模子图的起始点？
        // 这隐藏了一个拓扑排序 + 动态规划的思路在其中：
        // 如果想要减少上述重复计算过程，可以考虑使用动态规划，但是
        // 需要直到1,2,3以及后面节点谁在前谁在后的问题，使用拓扑排序解决
        // dp[v][c] 表示到达节点v的所有路径的颜色为c的最大值(并未统计v节点本身)
        // 对于u所有的 -> v: 
        // dp[v][c] = max(dp[u][c], dp[v][c]); // 广度优先遍历

        // 构建邻接表，统计入度情况
        vector<int> noInNode;
        int n = colors.size();
        vector<vector<int>> g(n);

        map<int, int> inDeg;
        for(auto &e : edges) {
            inDeg[e[1]]++;
            g[e[0]].emplace_back(e[1]);
        }
        
        // 做拓扑排序，首先找到那些个入度为0的点
        vector<array<int, 26>> dp(n);
        deque<int> q;
        for(int i = 0; i < n; ++i) {
            auto it = inDeg.find(i);
            if(it == inDeg.end()) {
                q.push_back(i);
            }
        }
        
        // bfs访问节点的数目超过n本身才能说明有环
        // 或者dfs能够访问到之前访问过的节点，也说明有环
        // 不能仅仅通过是否有出度为0的节点来判断是否成环，eg:
        // [[0,1],[1,1]]
        int bfsTravelNum = 0;
        // 使用bfs遍历获取拓扑排序顺便动态规划
        while(!q.empty()) {
            ++bfsTravelNum;
            // 取出一个没有入度的节点
            int u = q.front();
            q.pop_front();
            // 访问到u节点
            dp[u][colors[u] - 'a']++;

            // 更新所有 以v为终点的路径(不包含v本身) 的颜色为c的最大节点数
            for(int v : g[u]) {
                inDeg[v]--;
                for(int c = 0; c < 26; ++c) {
                    dp[v][c] = max(dp[v][c], dp[u][c]);
                }
                // 位于u拓扑排序后面的v
                if(0 == inDeg[v]) {
                    q.push_back(v);
                }
            }
        }
        
        if(bfsTravelNum != n) return -1;

        for(int i = 0; i < n; ++i) {
            ans = max(ans, *max_element(dp[i].begin(), dp[i].end()));
        }

        return ans;
    }
};

3 环路判断

1 bfs访问节点的数目超过n本身才能说明有环
2 或者dfs能够访问到之前访问过的节点，也说明有环
3 不能仅仅通过是否有出度为0的节点来判断是否成环，eg:
[[0,1],[1,1]]

influxDBInstall

Posted on 2021-11-23 Edited on 2023-08-03

1 docker-compose安装

version: "3.4"

# https://docs.influxdata.com/influxdb/v1.7/administration/config
services:
  influxdb:
    image: influxdb:1.7-alpine
    environment:
      - INFLUXDB_ADMIN_ENABLED=true 
      - INFLUXDB_ADMIN_USER=${INFLUXDB_ADMIN_USER:-root}
      - INFLUXDB_ADMIN_PASSWORD=${INFLUXDB_ADMIN_PASSWORD:-root}
      - INFLUXDB_DB=test
      - INFLUXDB_HTTP_LOG_ENABLED=false
      - INFLUXDB_REPORTING_DISABLED=true
      - INFLUXDB_USER=${INFLUXDB_USER:-test}
      - INFLUXDB_USER_PASSWORD=${INFLUXDB_USER_PASSWORD:-test}
    ports:
      - "8083:8083"
      - "8086:8086"
    deploy:
      mode: replicated
      replicas: 1
      resources:
        limits:
          memory: 2048M
        reservations:
          memory: 1024M
    volumes:
      - ./local_bind_volume_dir:/var/lib/influxdb

1.5 基本概念理解

https://www.cnblogs.com/yihuihui/p/11386679.html

2 基本操作

https://jasper-zhang1.gitbooks.io/influxdb/content/Guide/writing_data.html
插入一个值：

1
2
3

curl -i -X POST "http://localhost:8086/write?db=test" -u root:root --data-binary "cpu_load_short,host=server01,region=us-west value=0.64,value2=0.86 1434055562000000000"

> insert cpu_load_short,host=server02,region=de value=0.1,value2=0.2

从上面的输出，简单小结一下插入的语句写法:
insert + measurement + “,” + tag=value,tag=value + + field=value,field=value

tag与tag之间用逗号分隔；field与field之间用逗号分隔
tag与field之间用空格分隔
tag都是string类型，不需要引号将value包裹
field如果是string类型，需要加引号

查询该值：

> select * from cpu_load_short;
name: cpu_load_short
time                host     region  value value2
----                ----     ------  ----- ------
1434055562000000000 server01 us-west 0.64  0.86
1637648158355267700 server02 de      0.1   0.2

4 代码操作:

注意写入的过程需要保证有field，不能全为tag，将很多raw插入：(以下划线开始的为filed，filed字段不会建立索引，故查询慢)

    public void insert(String table, List<Map<String, Object>> rows) {
        if (CollectionUtils.isEmpty(rows)) {
            return;
        }
        List<Point> points = rows.stream()
                .filter(e -> !CollectionUtils.isEmpty(e))
                .map(e -> {
                        return to(table, e);

                })
                .collect(Collectors.toList());
        if (CollectionUtils.isEmpty(points)) {
            return;
        }
        BatchPoints batchPoints = BatchPoints.builder()
                .points(points)
                .build();
        influxDB.write(batchPoints);
        influxDB.flush();
    }

/** to函数 **/ 
    private Point to(String table, Map<String, Object> row)  {
        Point.Builder builder = Point.measurement(table).time(getTime(row), TimeUnit.MILLISECONDS);
        row.remove("time");
        row.forEach((k, v) -> {
            if (v == null) {
                return;
            }
            if (StringUtils.startsWith(k, "_")) {
                String key = StringUtils.removeStart(k, "_");
                if (v.getClass().getName().equals(boolean.class.getName())) {
                    builder.addField(key, (boolean) v);
                } else if (v.getClass().getName().equals(short.class.getName())) {
                    builder.addField(key, (short) v);
                } else if (v.getClass().getName().equals(int.class.getName())) {
                    builder.addField(key, (int) v);
                } else if (v.getClass().getName().equals(long.class.getName())) {
                    builder.addField(key, (long) v);
                } else if (v.getClass().getName().equals(float.class.getName())) {
                    builder.addField(key, (float) v);
                } else if (v.getClass().getName().equals(double.class.getName())) {
                    builder.addField(key, (double) v);
                } else if (v instanceof Boolean) {
                    builder.addField(key, (Boolean) v);
                } else if (v instanceof Number) {
                    builder.addField(key, (Number) v);
                } else if (v instanceof String) {
                    builder.addField(key, (String) v);
                } else {
                    builder.addField(key, v.toString());
                }
            } else {
                builder.tag(k, v.toString());
            }
        });
        return builder.build();
    }
    
/** build函数(influxdb官方维护) 将会检测是否含有field字段 **/ 
        public Point build() {
            Preconditions.checkNonEmptyString(this.measurement, "measurement");
            Preconditions.checkPositiveNumber(this.fields.size(), "fields size"); // 此处需保证fields size 大于等于1
            Point point = new Point();
            point.setFields(this.fields);
            point.setMeasurement(this.measurement);
            if (this.time != null) {
                point.setTime(this.time);
                point.setPrecision(this.precision);
            }

            point.setTags(this.tags);
            return point;
        }

lcMovingWindow - 滑动窗口 1

Posted on 2021-11-18 Edited on 2023-08-03

1 滑动窗口

priority_queue经常用

0480 滑动窗口中位数

1 题目

https://leetcode-cn.com/problems/sliding-window-median/

2 解题思路

1 使用一个multiset维护当前窗口，
- 1.1 不使用priority_queue的原因，无法删除元素
- 1.2 不使用map/set的原因，不能含有重复元素
2 对于窗口，维护一个中位数指针，注意到中位数指针在每一次窗口移动只会发生几种情况
- 2.1 向左，向右，不动
- 2.2 分类讨论清除即可

class Solution {
public:
    vector<double> medianSlidingWindow(vector<int>& nums, int k) {
        long long n = nums.size();
        std::multiset<long long, std::less<long long>> mySet(nums.begin(), nums.begin() + k);

        vector<double> res;
        multiset<long long>::iterator mid = mySet.begin();
        std::advance(mid, (k-1)/2);

        for(long long i = k; i <= n; ++i) {
            res.emplace_back((*mid + *next(mid, 1 - k%2))*1.0L/2);
            if(i == n) break;

            mySet.insert(nums[i]);
            if (nums[i] > *mid && nums[i - k] < *mid) {
                mid++;
                mySet.erase(mySet.lower_bound(nums[i-k]));
                continue;
                // std::advance(mid, 1);
            }

            if (nums[i] < *mid && nums[i - k] > *mid) {
                mid--;
                mySet.erase(mySet.lower_bound(nums[i-k]));
                continue;
                // std::advance(mid, -1);
            }
            // 7 3 7 7 4, k = 4
            // 7 8 7 7 4, k = 4
            if(nums[i-k] == *mid) {
                if(nums[i] >= *mid)  ++mid;
                else {
                    if(*prev(mid) != *mid) {
                        --mid;
                    }
                }
                mySet.erase(mySet.lower_bound(nums[i-k]));
                continue;
            } 

            if(nums[i] == *mid) {// 相当于一个比mid大的数字插入到了mid的前面
                if(nums[i-k] <= *mid)  ++mid;
                mySet.erase(mySet.lower_bound(nums[i-k]));
                continue;
            }
        }
        return res;
    }
};

0992 k个不同元素的子数组个数

1 题目

https://leetcode-cn.com/problems/subarrays-with-k-different-integers/submissions/

2 解题思路

1 正常思路：
- 1.1 首先窗口是必须的，即为[st, ed]，那么保证这个窗口时刻含有k个不同变量，然后求出来每个以ed为结尾的子数组的个数求和即可
- 1.2 那么以ed为结尾的窗口[st, ed]的子数组个数求法，假设k=2，窗口为1,2，1,2,那么以ed为结尾，st就向前移动，直到窗口内的不同元素个数减少到了k-1，此时st移动到第二个2的位置，一共移动了3次，也就是说以ed为结尾的含有k个不同变量的子数组个数为3。
- 1.3 其中的复杂之地在于：如何判断窗口内不同元素的个数，我们采用经典的空间换时间的方法(因为所有元素的值不会大于数组本身长度),用freq[val]记录val出现的次数，倘若长度不限呢？那就需要使用unordered_map来记录当前窗口所有元素的出现次数，然后每移动一次st需要遍历一遍这个map来判断当前窗口内不同元素的个数，那么整体复杂度为： o(n * k * k)
2 官方题解：
- 2.1 不同元素为k的子数组的个数为：不同元素最多为k的子数组个数 - 不同元素最多为k-1的子数组个数，那么问题转为求不同元素最多为k的一个数组它子数组的个数
- 2.2 求法：还是滑动窗口的思想，始终保持窗口中最多元素的个数不超过k（方式为每次移动ed，直到第一次超过k，然后移动st直到小于k），然后对于每个ed，ed - st就是以ed为窗口结尾对应的不同元素不超过k的子数组的个数，举个例子：(官方例子)：
  
  用具体的例子理解：最多包含 3 种不同整数的子区间 [1, 3, 2, 3] （双指针算法是在左边界固定的前提下，让右边界走到最右边），当前可以确定 1 开始的满足最多包含 3 种不同整数的子区间有 [1]、[1, 3]、[1, 3, 2]、[1, 3, 2, 3]。

class Solution {
public:
    int subarraysWithKDistinct(vector<int>& nums, int k) {
        return maxSubArrayNumForKDiff(nums, k) - maxSubArrayNumForKDiff(nums, k - 1);

    }

    int maxSubArrayNumForKDiff(vector<int>& nums, int k) {
        vector<int> freq(nums.size() + 1);
        long long res = 0;
        int st = 0;
        int ed = 0;
        int curCnt = 0;
        while(ed < nums.size()) {
            // 求每个ed对应得到的最多k个不同元素的子数组个数
            if(freq[nums[ed]] == 0) {
                curCnt ++;
            }
            freq[nums[ed]]++;
            ++ed;

            // 减小窗口到窗口内元素种类第一次为k-1个
            while(curCnt > k) {
                freq[nums[st]]--;
                if(freq[nums[st]] == 0) {
                    curCnt--;
                }
                ++st;
            }
            res += ed - st;
        }
        return res;
    }
};

0904 完全水果个数

1 题目

https://leetcode-cn.com/problems/fruit-into-baskets/

2 解题思路

1 正常思路：(于0904https://leetcode-cn.com/problems/fruit-into-baskets/实现)
- 1.1 首先窗口是必须的，即为[st, ed]，那么保证这个窗口时刻含有k个不同变量，然后求出来每个以ed为结尾的子数组的个数求和即可
- 1.2 那么以ed为结尾的窗口[st, ed]的子数组个数求法，假设k=2，窗口为1,2，1,2,那么以ed为结尾，st就向前移动，直到窗口内的不同元素个数减少到了k-1，此时st移动到第二个2的位置，一共移动了3次，也就是说以ed为结尾的含有k个不同变量的子数组个数为3。
- 1.3 其中的复杂之地在于：如何判断窗口内不同元素的个数，我们采用经典的空间换时间的方法(因为所有元素的值不会大于数组本身长度),用freq[val]记录val出现的次数，倘若长度不限呢？那就需要使用unordered_map来记录当前窗口所有元素的出现次数，然后每移动一次st需要遍历一遍这个map来判断当前窗口内不同元素的个数，那么整体复杂度为： o(n * k * (log k)) = o(n)
2 官方题解：
- 2.1 不同元素为k的子数组的个数为：不同元素最多为k的子数组个数 - 不同元素最多为k-1的子数组个数，那么问题转为求不同元素最多为k的一个数组它子数组的个数
- 2.2 求法：还是滑动窗口的思想，始终保持窗口中最多元素的个数不超过k（方式为每次移动ed，直到第一次超过k，然后移动st直到小于k），然后对于每个ed，ed - st就是以ed为窗口结尾对应的不同元素不超过k的子数组的个数，举个例子：(官方例子)：
  
  用具体的例子理解：最多包含 3 种不同整数的子区间 [1, 3, 2, 3] （双指针算法是在左边界固定的前提下，让右边界走到最右边），当前可以确定 1 开始的满足最多包含 3 种不同整数的子区间有 [1]、[1, 3]、[1, 3, 2]、[1, 3, 2, 3]。

class Solution {
public:
    int totalFruit(vector<int>& fruits) {
        if(fruits.size() <= 1) {
            return 1;
        }

        // 不同元素最多为2的数组长度
        int res = 0;
        int st = 0;
        int ed = 0;
        int curCnt = 0;
        map<int, int> freq;
        bool stNotMov = true;
        while(ed < fruits.size()) {
            while(freq.size() <= 2 && ed < fruits.size()) {
                if(freq.find(fruits[ed]) == freq.end()) {
                    curCnt++;
                }
                freq[fruits[ed]]++;
                ed++;
            }
            
            if(!stNotMov && ed != fruits.size()) {
                res = std::max(res, ed - st - 1);
            } else  {
                if(freq.size() == 3) {
                    res = std::max(res, ed - st - 1);
                } else {
                    res = std::max(res, ed - st);
                }
                
            }
            
            while(freq.size() > 2) {
                freq[fruits[st]]--;
                if(freq[fruits[st]] == 0) {
                    freq.erase(freq.find(fruits[st]));
                }
                ++st;
                stNotMov = false;
            }
        }
        return res;
    }
};

0995 执行次数最小: 每次翻转k个让数组全为1

1 题目

https://leetcode-cn.com/problems/minimum-number-of-k-consecutive-bit-flips/

2 解题思路

1 正常思路：窗口始终保持k个，去模拟翻转过程，由于需要在窗口内找到翻转后第一个为0的数字，这个复杂度为O（k），所以总复杂度为： O(n*k)
2 官方题解：使用差分数组diff,diff[i]表示nums[i]比nums[i-1]多了多少次翻转，那么当前总的翻转次数就为： sum(diff[i])，对于nums[i]而言， sum(diff[i])%2为0则表示nums[i]需要翻转。

class Solution {
public:
    int minKBitFlips(vector<int>& nums, int k) {
        vector<long long> preSum = {0};
        for(long long num : nums) {
            preSum.emplace_back(preSum.back() + num);
        }

        long long st = 0;
        long long ed = st + k - 1;
        long long n = nums.size();
        long long res = 0;

        vector<long long> diff(n+1);
        long long flipCnt = 0;
        // while(st < n - k + 1) {
            // 模拟思路会超时
            // if(nums[st] == 1) {
            //     ++st;
            //     continue;
            // }
            // int newSt = flipKBit(nums, k, st, preSum);
            // if(newSt == -1) {
            //     st = st + k;
            // } else {
            //     st = newSt;
            //     res += 1;
            // }
        // }
        // if(find(nums.end() - k, nums.end(), 0) == (nums.end())) {
        //     return res;
        // } 

        while(st < n) {
            // 采用查分数组记录每个元素应该翻转的次数
            // 这启发我们用差分数组的思想来计算当前数字需要翻转的次数。我们可以维护一个差分数组 \textit{diff}diff，其中 \textit{diff}[i]diff[i] 表示两个相邻元素 
            // \textit{nums}[i-1]nums[i−1] 和 \textit{nums}[i]nums[i] 的翻转次数的差，对于区间 [l,r][l,r]，将其元素全部加 11，只会影响到 ll 和 r+1r+1 处的差分值，
            // 故 \textit{diff}[l]diff[l] 增加 11，\textit{diff}[r+1]diff[r+1] 减少 11。
            flipCnt += diff[st];
            if((flipCnt + nums[st]) % 2 == 0) {
                if(st + k > n) {
                    return -1;
                }
                diff[st] ++;
                diff[st + k] --;
                res++;
                flipCnt ++;
            }
            ++st;
        }
        return res;
    }

    // 翻转kbit，返回第一个翻转窗口中反转后值不等于1的下标，否则返回-1
    int flipKBit(vector<int>& nums, int k, int st, vector<int>& preSum) {
        int firstNot1 = INT_MAX;
        // 需要O(k)时间的复杂度
        bool needFlip = find(nums.begin() + st, nums.begin() + st + k, 0) != (nums.begin() + st + k);
        // 使用前缀和优化，由于实地翻转了数组，于是会改变对应的前缀和，所以此方法行不通
        // bool needFlip = ((preSum[st + k] - preSum[st]) != k);

        // for(int i = st; i < k; ++i) {
        //     if(nums[st + i] != 1) {
        //         needFlip = true;
        //     }
        // }
        if(needFlip) {
            for(int i = 0; i < k; ++i) {
                nums[st + i] = abs(nums[st + i] - 1);
                if(nums[st + i] != 1) {
                    firstNot1 = min(firstNot1, st + i);
                }
            }
            return firstNot1 > nums.size() ? st + k : firstNot1 ;
        }
        

        return -1;
    }
};

1696 最大结果

1 题目

https://leetcode-cn.com/problems/jump-game-vi/submissions/

2 解题思路

1 采用动态规划：dp[i]表示跳到i处的最大收益,如下：搜索i的前k个下标即可

// o(n * k)解法
dp[0] = 0;
dp[1] = nums[0];
for(int i = 1; i < nums.size() + 1; ++i) {
    for(int m = 1; m < k + 1 && i - m > 0; ++m) {
        dp[i] = max(dp[i], dp[i-m] + nums[i-1]);
    }
}

2 优化上述搜索前k个下标的方案，我们采用优先队列来维护前k个中最大的上一跳：

将上述O(n*k)变为O(n*logk)，原因是maxHeap的push操作是logN的复杂度

class Solution {
public:
    struct number {
        long long idx = 0;
        long long val = 0;
        number(long long idx, long long val): idx(idx), val(val) {};

        // sort descending
        bool  operator<(const number& b) const {return this->val < b.val;}
    };
    int maxResult(vector<int>& nums, int k) {
        vector<long long> dp(nums.size() + 1, INT_MIN);
        // o(n * k)解法
        dp[0] = 0;
        dp[1] = nums[0];
        // for(int i = 1; i < nums.size() + 1; ++i) {
        //     for(int m = 1; m < k + 1 && i - m > 0; ++m) {
        //         dp[i] = max(dp[i], dp[i-m] + nums[i-1]);
        //     }
        // }

        std::priority_queue<number, std::vector<number>, std::less<number>> maxHeap;
        maxHeap.push({1, nums[0]});
        // 使用堆优化：
        for(int i = 2; i < nums.size() + 1; ++i) {
            while(maxHeap.top().idx < i - k) {
                maxHeap.pop();
            }

            dp[i] =  maxHeap.top().val + nums[i - 1];
            maxHeap.push({i, dp[i]});
            
            // for(int m = 1; m < k + 1 && i - m > 0; ++m) {
            //     dp[i] = max(dp[i], dp[i-m] + nums[i-1]);
            // }
        }
        
        return dp[nums.size()];

    }
};

总结

滑动窗口的最大值：可以使用maxHeap来维护，复杂度logk

lcPrefixSum - 前缀和 1

Posted on 2021-11-18 Edited on 2023-08-03

1 前缀和

vector<int> prefSum {nums[0]};
for(int i = 1; i < nums.size(); ++i) {
    prefSum[i] += (nums[i] + prefSum.back()); 
}

1546最大非重叠数组

1 题目

https://leetcode-cn.com/problems/maximum-number-of-non-overlapping-subarrays-with-sum-equals-target/submissions/

2 解题思路

最为关键的一句话：
每次找结束序号最小的和为target的子数组，然后从这个子数组的后面开始搜寻下一个子数组，经典贪心。

前缀和，普通为o(n^2)，使用hash优化：
subSum[j:i]，本来需要遍历所有的j找出为k的subarray，
但是换个思路：其实就是找i之前，有多少个前缀和为 preSum[j] - k，
那么我们把前缀和用hash存一下，那不就能够很快找到了？

但是有一个问题，在下一次搜寻开始的时候，需要将上一次搜寻过程的hash清零，
否则上一次的hash的结果会影响当前子序和。
而且假设上一次搜寻到j了，那么这次从j+1开始搜寻，必须保证前缀和也是从j+1开始

class Solution {
public:
    int maxNonOverlapping(vector<int>& nums, int target) {
        int ans = 0;
        // vector<int> preSum(nums.size());

        // preSum[0] = nums[0];
        // for(int i = 1; i < nums.size(); ++i ){
        //     preSum[i] = preSum[i-1] + nums[i];
        // }
        // while(ed < nums.size()) {
        //     for(int st = lastFoundEd; st <= ed; ++st) {
        //         if(preSum[ed] - preSum[st] + nums[st] == target) {
        //             ++ans;
        //             lastFoundEd = ed+1;
        //             break;
        //         }
        //     }
        //     ++ed;
        // }

        int st = 0;
        int ed = 0;
        int lastFoundEd = ed;

        // map<int, int> hash;

        
        while(st < nums.size()) {
            ed = st;
            // hash.clear();   // clear history to avoid repeat count
            unordered_set<int> hash = {0};
            int curSumFromLastFoundEd = 0;
            while(ed < nums.size()) {
                curSumFromLastFoundEd += nums[ed];
                if(hash.count(curSumFromLastFoundEd - target)) {
                    ++ans;
                    st = ed;        // new search start
                    break;
                } else {
                    hash.insert(curSumFromLastFoundEd);
                }
                ++ed;
            }
            ++st;
        }

        return ans;
    }
};

0560subArraySum 子数组和为k

1 题目

https://leetcode-cn.com/problems/subarray-sum-equals-k/

2 解题思路

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        vector<int> prefSum(nums.size());
        prefSum[0] = nums[0];
        for(int i = 1; i < nums.size(); ++i) {
            prefSum[i] += (nums[i] + prefSum[i-1]); 
        }

        int st = 0;
        int ed = 0;
        int ans = 0;
        int curSum = 0;
        std::unordered_map<int, int> hash;
        hash[0] = 1;
        while(ed < nums.size()) {
            if(hash.find(prefSum[ed] - k) != hash.end()) {
                ans += hash[prefSum[ed] - k];
            } 
            hash[prefSum[ed]]++;

            
            // for(int st = ed; st >= 0; --st) {
            //     curSum = prefSum[ed] - prefSum[st] + nums[st];
            //     if(curSum == k){
            //         ++ans;
            //     }
            // }
            ++ed;
        }
        
        return ans;
    }
};

1171移除和为0的子链表

1 题目：

https://leetcode-cn.com/problems/remove-zero-sum-consecutive-nodes-from-linked-list/

2 解题思路：

个人暴力思路：

1 每次移除一个和为0的子数组，返回一个新的链表
2 重复上述过程直到没有和为0的子数组

前缀和思路参考：
采用前缀和判断和为0方法：
我们可以考虑如果给的入参不是链表是数组的话，只需要求出前缀和，对于前缀和相同的项，那他们中间的部分即是可以消除掉的，比如以 [1, 2, 3, -3, 4] 为例，其前缀和数组为 [1, 3, 6, 3, 7] ，我们发现有两项均为 3，则 6 和第二个 3 所对应的原数组中的数字是可以消掉的。

class Solution {
public:
    ListNode* newHead;

    ListNode* removeZeroSumSublists(ListNode* head) {
        newHead = head;
        while(removeOneZeroSubList(newHead)){ }
        return newHead;
    }

    bool removeOneZeroSubList(ListNode* newHead) {
        vector<int> valVec;
        ListNode* head = newHead;
        ListNode* p = head;
        while(p != nullptr) {
            valVec.emplace_back(p->val);
            p = p->next;
        }
        size_t len = valVec.size();
        vector<vector<int>> sumMat(len, vector<int>(len));

        // cal all the sub len
        // sumMat[a, b] = sumMat[a, b-1] + a
        ListNode* stPtr = head;
        ListNode* lastStPtr = nullptr;
        for(int st = 0; st < len; ++st) {
            sumMat[st][st] = valVec[st];
            if(sumMat[st][st] == 0) {
                if(nullptr == lastStPtr) {
                    this->newHead = head->next;
                    return true;
                }
                lastStPtr->next = stPtr->next;
                return true;
            }
            ListNode* edPtr = stPtr->next;
            for(int ed = st + 1; ed < len; ++ed) {
                sumMat[st][ed] = sumMat[st][ed-1] + valVec[ed];
                if(sumMat[st][ed] == 0) {
                    if(nullptr == lastStPtr) {
                        this->newHead = edPtr->next;
                        return true;
                    }
                    lastStPtr->next = edPtr->next;
                    return true;
                }
                edPtr = edPtr->next;
            }
            lastStPtr = stPtr;
            stPtr = stPtr->next;
        }
        return false;
    }
};

1292最大方块长度

1 题目

https://leetcode-cn.com/problems/maximum-side-length-of-a-square-with-sum-less-than-or-equal-to-threshold/

2 解题思路

1 建立二维前缀和：

  vector<vector<int>> preSum(m+1, vector<int>(n+1, 0));
for(int i = 1; i < m+1; ++i) {
    for(int j = 1; j < n+1; ++j) {
        preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] - preSum[i-1][j-1] + mat[i-1][j-1];
    }
}

2 遍历所有边长的正方形即可(每个正放形为起点加上边长)，遍历长度的过程可以通过二分搜索加速

值得思考的点：
如何快速得知当前位置是不是被阻挡了？
使用unordered_set作为hash快速查找

class Solution {
public:
    int maxSideLength(vector<vector<int>>& mat, int threshold) {
        // mat.row >= m > i >= 0, mat.col >= n > j >= 0
        // preSum[m][n] -> preSum[i][j] = preSum[m][n] - preSum[m][j] - preSum[i][n] + preSum[i][j];
        int m = mat.size();
        int n = mat[0].size();
        vector<vector<int>> preSum(m+1, vector<int>(n+1, 0));
        for(int i = 1; i < m+1; ++i) {
            for(int j = 1; j < n+1; ++j) {
                preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] - preSum[i-1][j-1] + mat[i-1][j-1];
            }
        }

        // traverse all square
        int maxSquareLen = std::min(m, n);
    //    for(int len = maxSquareLen; len >= 1; --len) { // len could be binary search
    //         for(int i = 0; i <= m - len; ++i) {
    //             for(int j = 0; j <= n - len; ++j) {
    //                 if(getRec(preSum, i+1, j+1, i + len, j + len) <= threshold) {
    //                     return len;
    //                 };
    //             }
    //         }
    //    }
        int stLen = 1;
        int edLen = maxSquareLen;
        int ans = 0;
        while(stLen <= edLen) {
            int len = (stLen + edLen) / 2;
            bool found = false;
            for(int i = 0; i <= m - len; ++i) {
                for(int j = 0; j <= n - len; ++j) {
                    if(getRec(preSum, i+1, j+1, i + len, j + len) <= threshold) {
                        found = true;
                    };
                }
            }
          
            if(found) { // len too small
                stLen = len+1;
                ans = len;
            } else { // len too big
                edLen = len-1;
            }
          
        }

        return ans;
    }

    int getRec(vector<vector<int>>& preSum, int i, int j, int m, int n) {
        return preSum[m][n] - preSum[m][j-1] - preSum[i-1][n] + preSum[i-1][j-1];
    }
};

1124 良好表现的最长时间段

1 题目

https://leetcode-cn.com/problems/longest-well-performing-interval/

2 解题思路

较为容易想到前缀和思路：
不好想的地方在于第1和3条，思路如下：

1 对于这种良好费良好的判断，我们需要把数组转换成 -1, 1的数组
2 对上述数组作前缀和
3 那么对于每个到来的j，只需要找到最小的i，满足 preSum[j] - preSum[i] == 1即可
- 3.1 如何理解最小的i，也就是说，对于同一个preSum值的下标，我们总是去最小的i即可
- 3.2 对于 9 9 9 9 9这种全正常的思路，如何判断？前缀和的值本身就可以判断，大于零的下标都可以是良好工作区间

class Solution {
public:
    int longestWPI(vector<int>& hours) {
        vector<int> preSum = {0};
        for(int i = 0; i < hours.size(); ++i) {
            preSum.emplace_back((hours[i] > 8 ? 1 : -1) + preSum.back());
        }
          
        int st = 0;
        int ed = 0;
        int res = INT_MIN;
        // key: presum's value, value: presum's index
        map<int, int> m;
        m[0] = 0;
        int lastPop = 0;
        vector<int> mono = {0};
        for(; ed < hours.size(); ++ed) {
            if (preSum[ed + 1] > 0) {
                res = std::max(res, ed + 1);
                continue;
            }
            map<int, int>::iterator it = m.find(preSum[ed + 1] - 1);
            if(it != m.end()) {
                res = std::max(ed - it->second, res);
            } 
            if (m.find(preSum[ed + 1]) == m.end()) {
                m[preSum[ed + 1]] = ed; 
            }
            
        }
        return res < 0 ? 0 : res;

    }
};